Exercice : Résoudre 5
Question
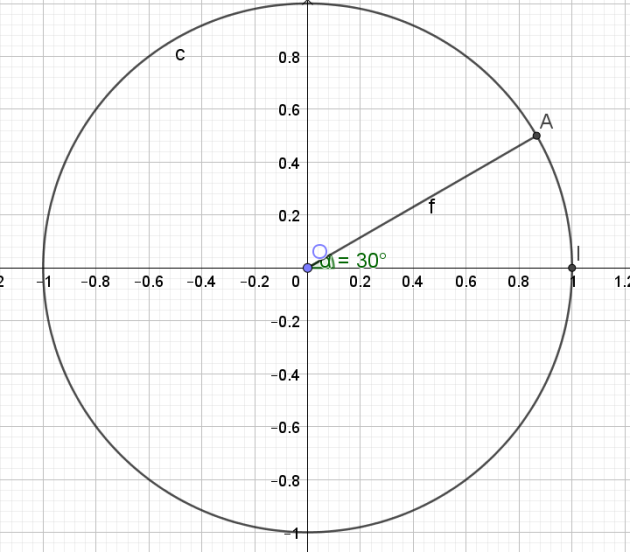
1. a.Construire le point A tel que OA=1 et \(\left(\overrightarrow{OI},\overrightarrow{OA}\right)=\dfrac{\pi}{6}\)
sur le cercle trigonométrique.
Question
b. Donner la valeur exacte du nombre réel \(\cos\left(\dfrac{\pi}{6}\right)\)
Solution
\(\cos\left(\dfrac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\)
Question
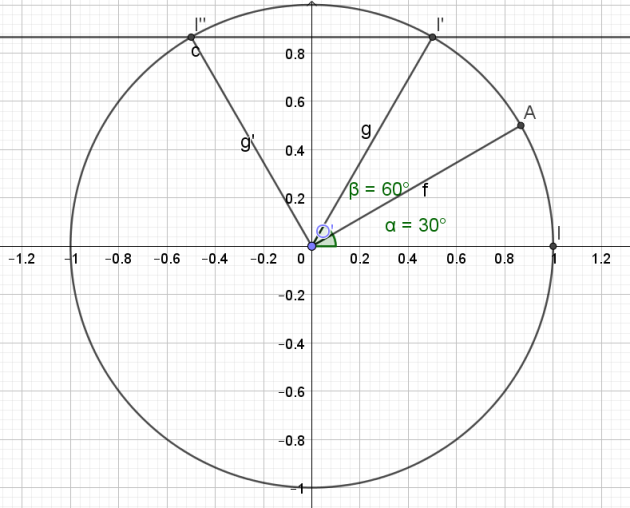
c. Résoudre dans l'ensemble \(\mathbb{R}\) des nombres réels l'équation \(\sin\left(x\right)=\cos\left(\dfrac{\pi}{6}\right)\).
Représenter les solutions de l'équation précédente sur le cercle trigonométrique.
Solution
\(\sin\left(x\right)=\cos\left(\dfrac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\).
\(\begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\pi-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\frac{3\pi}{3}-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Question
2. Résoudre dans l'ensemble \(\mathbb{R}\) des nombres réels l'équation \(\sin\left(2x\right)=\cos\left(\dfrac{\pi}{6}\right)\).
Solution
\(\sin\left(2x\right)=\cos\left(\dfrac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\).
\(\begin{cases}2x=\frac{\pi}{3}+2k\pi\\2x=\pi-\frac{\pi}{3}+2\kpi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}2x=\frac{\pi}{3}+2k\pi\\2x=\frac{3\pi}{3}-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+k\pi\\2x=\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+k\pi\\x=\frac{2\pi}{6}+k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+k\pi\\x=\frac{\pi}{3}+k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Pour k=0
\(\begin{cases}x=\frac{\pi}{6}\\x=\frac{\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
Pour k=1
\(\begin{cases}x=\frac{\pi}{6}+\pi\\x=\frac{2\pi}{3}+\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+\frac{6\pi}{6}\\x=\frac{2\pi}{3}+\frac{3\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{7\pi}{6}\\x=\frac{5\pi}{3}\end{cases}\)
Ces valeurs ne sont pas comprises dans l'intervalle \(]-\pi ;pi]\)
Inutile de prendre des valeurs de k plus grandes
Pour k=-1
\(\begin{cases}x=\frac{\pi}{6}-\pi\\x=\frac{\pi}{3}-\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}-\frac{6\pi}{6}\\x=\frac{\pi}{3}-\frac{3\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-5\pi}{6}\\x=\frac{-2\pi}{3}\end{cases}\)
Ces valeurs sont comprises dans l'intervalle \(]-\pi ;pi]\)
Pour k=-2
\(\begin{cases}x=\frac{\pi}{6}-2\pi\\x=\frac{\pi}{3}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}-\frac{12\pi}{6}\\x=\frac{\pi}{3}-\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-11\pi}{6}\\x=\frac{-5\pi}{3}\end{cases}\)
Ces valeurs ne sont pas comprises dans l'intervalle \(]-\pi ;pi]\)
Inutile de prendre des valeurs de k plus petites
Les mesures principales sont donc
\(\begin{cases}x=\frac{\pi}{6}\\x=\frac{\pi}{3}\\x=\frac{-5\pi}{6}\\x=\frac{-2\pi}{3}\end{cases}\)
Question
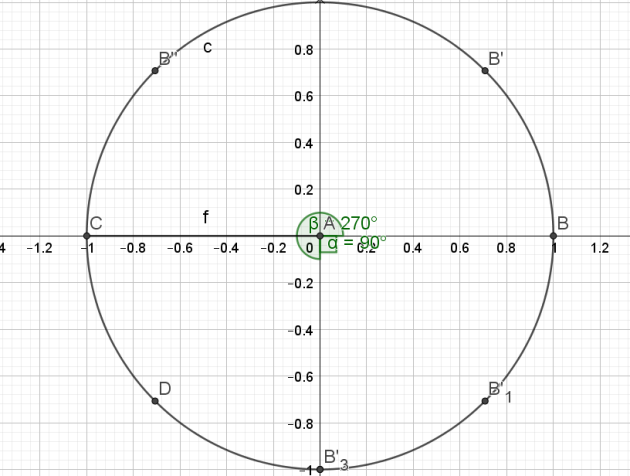
3. Soit a un nombre réel appartenant à l'intervalle \(\left[0;\pi\right]\).On considère l'équation\(\sin\left(x\right)=\cos\left(a\right)\).
Solution
\(-sin^2 x = 1\)
\(\iff sin^2 x = -1\)
or un carré est toujours positif donc \(S=\emptyset\)
Question
a. Pour quelles valeurs de a l'ensemble des solutions de l'équation précédente est-il représenté par un unique point du cercle trigonométrique?
Question
b. Écrire un algorithme qui fournit le nombre de points du cercle trigonométrique représentant les solutions de l'équation précédente lorsqu'on lui donne, en entrée, la valeur du nombre a.