Exercice : Résoudre 10
Résoudre les équations suivantes :
Question
\(cos(x)=\frac{-\sqrt{3}}{2}\)
Solution
\(cos(x)=\frac{-\sqrt{3}}{2}\)
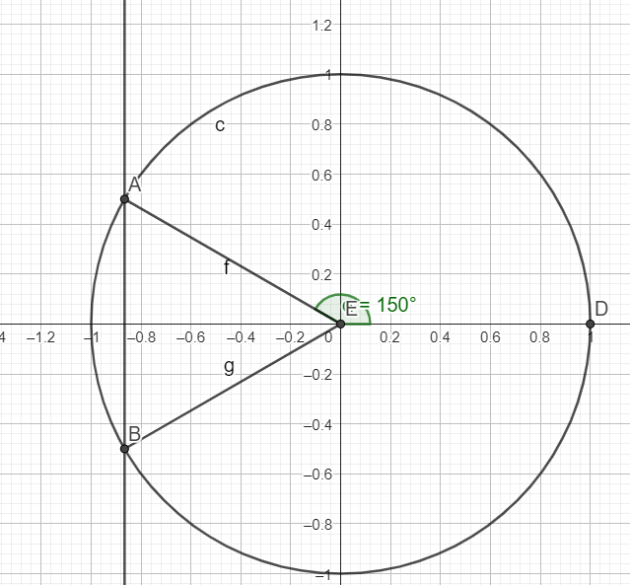
Les solutions dans \(\mathbb{R}\) sont :
\(S=\{\frac{2\pi}{3}+2\pi \times k ;\frac{4\pi}{3}+2\pi \times k\}\)
avec \(k \in \mathbb{Z}\)
Question
2. \(2sin^2(x)-sin(x)=1\)
Solution
On effectue le changement de variable :
\(X= sin(x)\)
On obtient alors l'équation :
\(2X^2-X=1\)
\(\iff 2X^2-X-1=0\)
Cette équation est une équation du second degré, on calcule son discriminant :
\(a=2\) \(b=-1\) et \(c=-1\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-1)^2-4 \times 2 \times (-1)\)
\(\iff \Delta=1+8\)
\(\iff \Delta=9\)
Comme \(\Delta\)>0 ,l'équation \(2X^2-X-1=0\) admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-(-1)-\sqrt{9}}{2 \times 2}\\X_2=\frac{-(-1)+\sqrt{9}}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{1-3}{4}\\X_2=\frac{1+3}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2}{4}\\X_2=\frac{4}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-1}{2}\\X_2=1\end{cases}\)
\(\iff \begin{cases}X_1=sin(x_1)=\frac{-1}{2}\\X_2=sin(x_2)=1\end{cases}\)
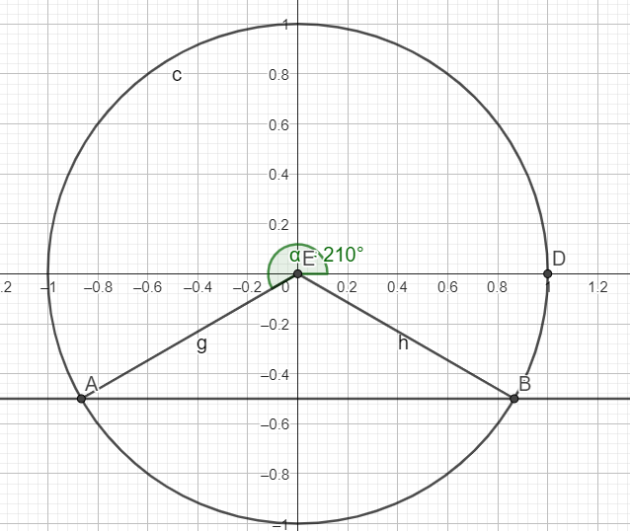
\(X_1=sin(x_1)=\frac{-1}{2}\)
Les solutions dans \(\mathbb{R}\) sont :
\(S=\{\frac{7\pi}{6}+2\pi \times k ;\frac{11\pi}{6}+2\pi \times k\}\)
avec \(k \in \mathbb{Z}\)
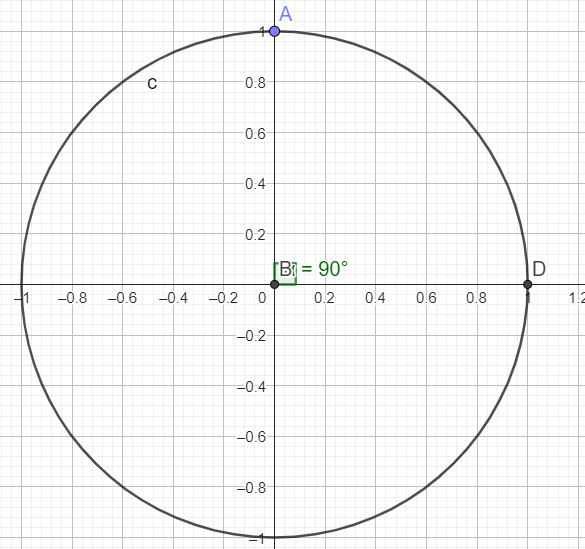
\(X_2=sin(x_2)=1\)
Les solutions dans \(\mathbb{R}\) sont :
\(S=\{\frac{\pi}{2}+2\pi \times k \}\)
avec \(k \in \mathbb{Z}\)
Finalement les solutions sont :
\(S=\{\frac{\pi}{2}+2\pi \times k ;\frac{7\pi}{6}+2\pi \times k ;\frac{11\pi}{6}+2\pi \times k\}\)
avec \(k \in \mathbb{Z}\)
Question
3. \(cos^2(x)-2cos(x)+1=0\)
Solution
On effectue le changement de variable :
\(X= cos(x)\)
On obtient alors l'équation :
\(X^2-2X+1=0\)
Cette équation est une équation du second degré, on calcule son discriminant :
\(a=1\) \(b=-2\) et \(c=1\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-2)^2-4 \times 1\times 1\)
\(\iff \Delta=4-4\)
\(\iff \Delta=0\)
Comme \(\Delta\)=0 ,l'équation \(X^2-2X+1=0\) admet une unique solution :
\(X_0=\frac{-b}{2a}=\frac{-(-2)}{2 \times 1}=\frac{2}{2}=1\)
\(\iff X_0= cos(x_0)=1\)
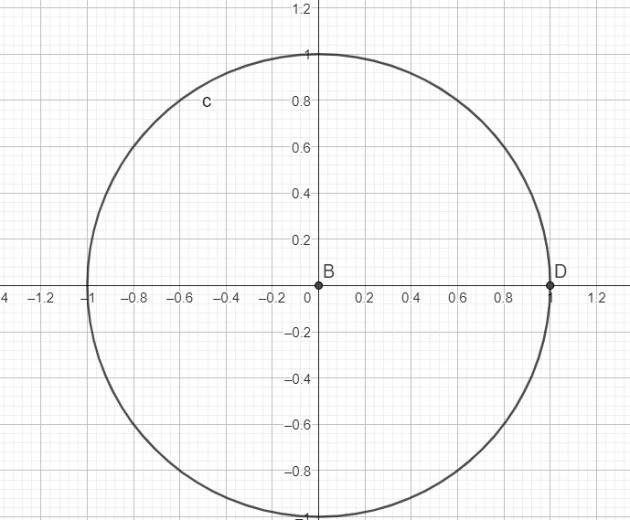
Finalement les solutions sont :
\(S=\{0+2\pi \times k \}=\{2\pi \times k \}\)
avec \(k \in \mathbb{Z}\)
Question
4.\( -cos^2(y)-3sin(y)+3=0\)
Solution
\(-cos^2(y)-3sin(y)+3=0\)
On sait que \(cos^2(y)+sin^2(y)=1\) pour tout \(y \in \mathbb{R}\)
donc \(cos^2(y)=1-sin^2(y)\) pour tout \(y \in \mathbb{R}\)
et \(-cos^2(y)=-1+sin^2(y)\) pour tout \(y \in \mathbb{R}\)
\(-cos^2(y)-3sin(y)+3=0\)
\(\iff -1+sin^2(y)-3sin(y)+3=0\)
\(\iff sin^2(y)-3sin(y)+2=0\)
On effectue le changement de variable :
\(Y= sin(y)\)
On obtient alors l'équation :
\(Y^2-3Y+2=0\)
Cette équation est une équation du second degré, on calcule son discriminant :
\(a=1\) \(b=-3\) et \(c=2\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-3)^2-4 \times 1\times 2\)
\(\iff \Delta=9-8\)
\(\iff \Delta=1\)
Comme \(\Delta\)>0 ,l'équation \(Y^2-3Y+2=0\) admet deux solutions :
\(\begin{cases}Y_1=\frac{-b-\sqrt{\Delta}}{2a}\\Y_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{-(-3)-\sqrt{1}}{2 \times 1}\\X_2=\frac{-(-3)+\sqrt{1}}{2 \times 1}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{3-1}{2}\\Y_2=\frac{3+1}{2}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{2}{2}\\Y_2=\frac{4}{2}\end{cases}\)
\(\iff \begin{cases}Y_1=1\\Y_2=2\end{cases}\)
\(\iff \begin{cases}Y_1=sin(y_1)=1\\Y_2=sin(y_2)=2\end{cases}\)

\(Y_1=sin(y_1)=1\)
Les solutions dans \(\mathbb{R}\) sont :
\(S=\{\frac{\pi}{2}+2\pi \times k \}\)
avec \(k \in \mathbb{Z}\)
\(Y_2=sin(y_2)=2\) n'a pas de solution car une valeur de sinus est compris entre [-1 ;1]
Finalement les solutions dans \(\mathbb{R}\) sont :
\(S=\{\frac{\pi}{2}+2\pi \times k \}\)
avec \(k \in \mathbb{Z}\)