Exercice : Exercice 1
On considère le triangle ABC rectangle en B représenté ci-dessous :
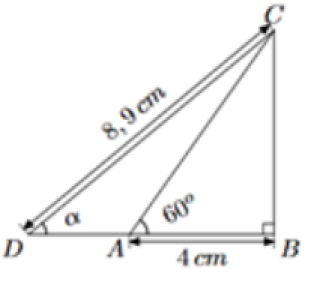
Question
1.Déterminer la longueur du segment [BC] arrondie au millimètre près
Solution
\(tan(60)=\frac{côté opposé}{côté adjacent}\)
\(\iff tan(60)=\frac{BC}{AB}\)
\(\iff tan(60)=\frac{BC}{AB}\)
\(\iff tan(60)=\frac{BC}{4}\)
\(\iff BC=4 \times tan(60)\simeq 6,92\)
Question
2.En déduire la mesure de l'angle \(\widehat{CDB}\) arrondie au degré près.
Solution
\(sin(\alpha)=\frac{côté opposé}{hypoténuse}\)
\(\iff sin(\alpha)=\frac{BC}{CD}\)
\(\iff sin(\alpha)=\frac{4 \times tan(60)}{8,9}\)
\(\iff sin(\alpha)=\frac{4 \times tan(60)}{8,9}\)
\(\iff sin(\alpha) \simeq 0,778\)
\(\iff \alpha \simeq Arcsin(0,778)\)
\(\iff \alpha \simeq 51°\)