Exercice : Exercice 9
Donner, sous forme de de réunions d'intervalles,
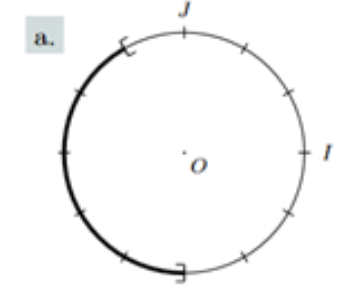
l'ensemble formé par les mesures principales des angles représentant les points surlignés du cercle trigonométrique :
Question
Solution
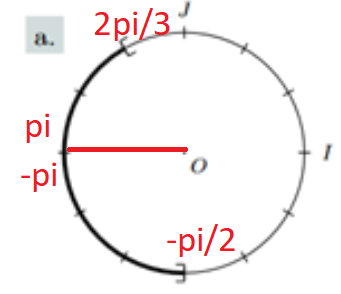
\(]-\pi ;-\frac{\pi}{2}] \cup ]\frac{2\pi}{3} ;\pi]\)
Question
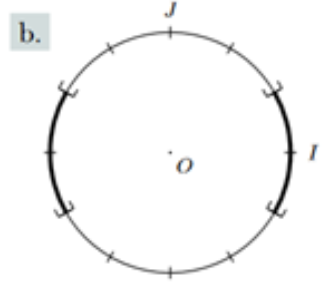
Solution
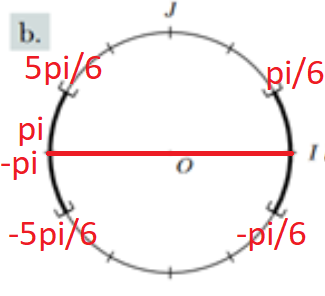
\(]-\pi ;-\frac{5\pi}{6}]\cup[-\frac{\pi}{6} ;\frac{\pi}{6}[\cup]\frac{5\pi}{6} ;\pi]\)
Pour chaque question, surligner l'ensemble des points ayant pour angle orienté l'ensemble précisé :
Question
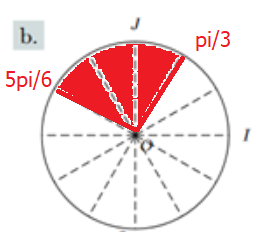
\([\frac{13\pi}{3} ;\frac{29\pi}{6}]\)
Solution
\(\frac{\frac{13\pi}{3}}{2\pi}\)
\(=\frac{13\pi}{3} \times \frac{1}{2\pi}\)
\(=\frac{13}{6}\)
\(2\le\frac{13}{6}\le3\)
\(\frac{13\pi}{3}-2 \times 2 \pi\)
\(=\frac{13\pi}{3}-4\pi\)
\(=\frac{13\pi}{3}-\frac{12\pi}{3}\)
\(=\frac{\pi}{3}\)
\(\frac{\frac{29\pi}{6} }{2\pi}\)
\(=\frac{29\pi}{6} \times \frac{1}{2\pi}\)
\(=\frac{29}{12}\)
\(2\le\frac{29}{12}\le3\)
\(\frac{29\pi}{6}-2 \times 2 \pi\)
\(=\frac{29\pi}{6}-4\pi\)
\(=\frac{29\pi}{6}-\frac{24\pi}{6}\)
\(=\frac{5\pi}{6}\)
\(\frac{29\pi}{6}-\frac{13\pi}{3}\)
\(=\frac{29\pi}{6}-\frac{26\pi}{6}\)
\(=\frac{3\pi}{6}=\frac{\pi}{2}\)
donc les deux angles appartiennent au même tour
et sont séparés de \(\frac{\pi}{2}\).
Question
\([\frac{\pi}{2} ;\frac{8\pi}{3}]\)
Solution
\(\frac{\pi}{2} \in]-\pi ;\pi]\)
donc il s'agit déjà de la mesure principale.
\(\frac{\frac{8\pi}{3}}{2\pi}\)
\(=\frac{8\pi}{3} \times \frac{1}{2\pi}\)
\(=\frac{8}{6}\)
\(1\le\frac{8}{6}\le2\)
\(\frac{8\pi}{3}-1 \times 2 \pi\)
\(=\frac{8\pi}{3}-2\pi\)
\(=\frac{8\pi}{3}-\frac{6\pi}{3}\)
\(=\frac{2\pi}{3}\)
\(\frac{8\pi}{3}-\frac{\pi}{2} \)
\(=\frac{16\pi}{6}-\frac{3\pi}{6}\)
\(=\frac{13\pi}{6}=2\pi+\frac{\pi}{6}\)
Les deux angles n'appartiennent donc pas
au même tour et sont séparés de \(\frac{13\pi}{6}\).