Exercice : Exercice 2
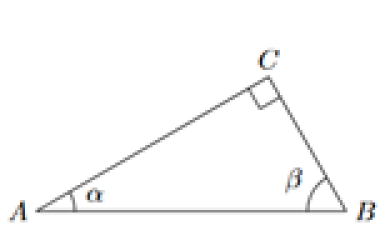
On considère un triangle ABC rectangle en C.
On note \(\alpha=\widehat{CAB}\) ; \(\beta=\widehat{ABC}\).
Question
1.Justifier que les angles \(\widehat{CAB}\) et \(\widehat{CBA}\) sont deux angles complémentaires.
Solution
\(\color{red}{\text{La somme des mesures des trois angles d'un triangle vaut 180°}}\)
donc
\(\widehat{CAB} + \widehat{CBA} + \widehat{BCA}=\pi\)
\(\iff \widehat{CAB} + \widehat{CBA} + \frac{\pi}{2}=\pi\)
\(\iff \widehat{CAB} + \widehat{CBA}=\pi-\frac{\pi}{2}\)
\(\iff \widehat{CAB} + \widehat{CBA}=\frac{\pi}{2}\)
\(\iff \widehat{\alpha} + \widehat{\beta}=\frac{\pi}{2}\)
\(\color{red}{\text{Deux angles sont dits complémentaires s'ils forment un angle droit (90°)}}\)
\(\widehat{CAB}\) et \(\widehat{CBA}\) sont donc deux angles complémentaires.
Question
2.a A l'aide des longueurs des côtés du triangle ABC, exprimer les valeurs de \(cos(\alpha)\) et \(sin(\beta)\)
Solution
\(cos(\alpha)=\frac{côté adjacent}{hypoténuse}=\frac{AC}{AB}\)
\(sin(\beta)=\frac{côté opposé}{hypoténuse}=\frac{AC}{AB}\)
Question
b.En déduire l'égalité :
\(cos(\alpha)=sin(\frac{\pi}{2}-\alpha)\)
Solution
\(cos(\alpha)=sin(\beta)\)
\(\iff cos(\alpha)=sin(\frac{\pi}{2}-\alpha)\)
Question
3.a.A l'aide des longueurs des côtés du triangle ABC, exprimer les valeurs de \(tan(\alpha)\) et \(tan(\beta)\)
Solution
\(tan(\alpha)=\frac{côté opposé}{côté adjacent}=\frac{CB}{AC}\)
\(tan(\beta)=\frac{côté opposé}{côté adjacent}=\frac{AC}{CB}\)
Question
b.En déduire l'égalité :
\(tan(\frac{\pi}{2}-\alpha)=\frac{1}{tan(\alpha)}\)
Solution
\(tan(\beta)=\frac{1}{tan(\alpha)}\)
donc
\(tan(\frac{\pi}{2}-\alpha)=\frac{1}{tan(\alpha)}\)
Question
4. Etablir l'égalité :
\((cos(\alpha))^2+(sin(\alpha))^2=1\)
Solution
\((cos(\alpha))^2+(sin(\alpha))^2=(\frac{AC}{AB})^2+(\frac{BC}{AB})^2\)
\(\iff (cos(\alpha))^2+(sin(\alpha))^2=\frac{AC^2}{AB^2}+\frac{BC^2}{AB^2}\)
\(\iff (cos(\alpha))^2+(sin(\alpha))^2=\frac{AC^2+BC^2}{AB^2}\)
Le triangle ABC est rectangle en C, d'hypoténuse AB
donc d'après le théorème de Pythagore :
\(AB^2=AC^2+BC^2\)
\(\iff (cos(\alpha))^2+(sin(\alpha))^2=\frac{AB^2}{AB^2}=1\)