Exercice : Exercice 11
Dans \(\mathbb{R}\) puis dans l'intervalle des mesures principales, résoudre les équations suivantes :
Question
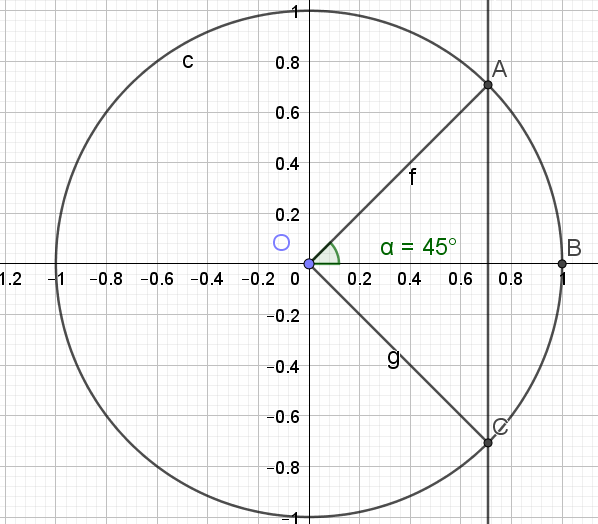
1.\(sin(x)=\frac{1}{2}\)
Solution
\(sin(x)=\frac{1}{2}\)
\(sin(x)=sin(\frac{\pi}{6})\)
\(\begin{cases}x=\frac{\pi}{6}+2k\pi\\x=\pi-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+2k\pi\\x=\frac{6\pi}{6}-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\iff \begin{cases}x=\frac{\pi}{6}+2k\pi\\x=\frac{5\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{\pi}{6}\\x=\frac{5\pi}{6}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{6}+2\pi\\x=\frac{5\pi}{6}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+\frac{12\pi}{6}\\x=\frac{5\pi}{6}+\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{13\pi}{6}\\x=\frac{17\pi}{6}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{6}-2\pi\\x=\frac{5\pi}{6}-2\pi\end{cases}\)
\(\begin{cases}x=\frac{\pi}{6}-\frac{12\pi}{6}\\x=\frac{5\pi}{6}-\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{-11\pi}{6}\\x=\frac{-7\pi}{6}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus
petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{\pi}{6}\\x=\frac{5\pi}{6}\end{cases}\)
Question
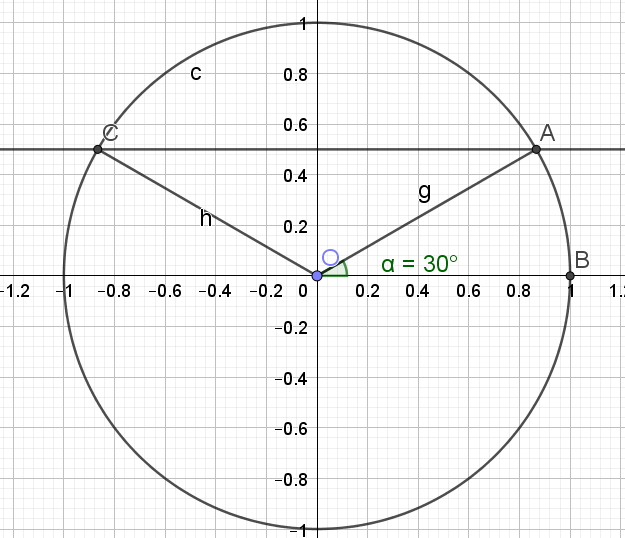
2.\(cos(x)=\frac{1}{2}\)
Solution
\(cos(x)=\frac{1}{2}\)
\(cos(x)=cos(\frac{\pi}{3})\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\begin{cases}x=\frac{\pi}{3}+2k\pi\\x=-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{\pi}{3}\\x=-\frac{\pi}{3}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{3}+2\pi\\x=-\frac{\pi}{3}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{3}+\frac{6\pi}{3}\\x=-\frac{\pi}{6}+\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{7\pi}{3}\\x=\frac{5\pi}{3}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{3}-2\pi\\x=-\frac{\pi}{3}-2\pi\end{cases}\)
\(\begin{cases}x=\frac{\pi}{3}-\frac{6\pi}{3}\\x=-\frac{\pi}{3}-\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-5\pi}{3}\\x=\frac{-7\pi}{3}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus
petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{\pi}{3}\\x=-\frac{\pi}{3}\end{cases}\)
Question
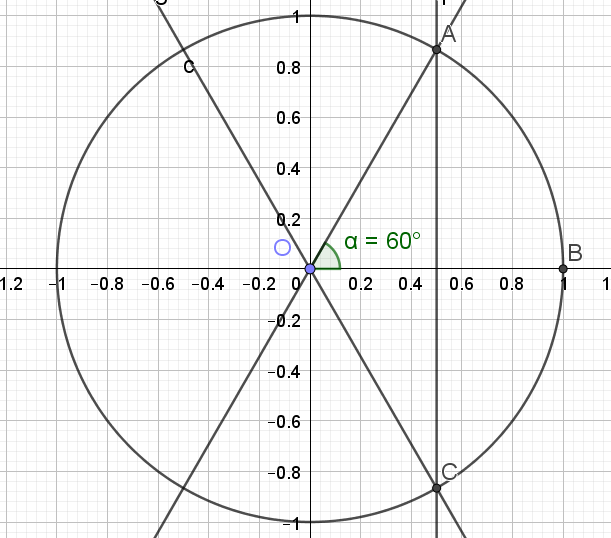
3.\(sin(x)=\frac{\sqrt{3}}{2}\)
Solution
\(sin(x)=\frac{\sqrt{3}}{2}\)
\(sin(x)=sin(\frac{\pi}{3})\)
\(\begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\pi-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\frac{3\pi}{3}-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\iff \begin{cases}x=\frac{\pi}{3}+2k\pi\\x=\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{\pi}{3}\\x=\frac{2\pi}{3}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{3}+2\pi\\x=\frac{2\pi}{3}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{3}+\frac{6\pi}{3}\\x=\frac{2\pi}{3}+\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{7\pi}{3}\\x=\frac{8\pi}{3}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{3}-2\pi\\x=\frac{2\pi}{3}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{3}-\frac{6\pi}{3}\\x=\frac{2\pi}{3}-\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-5\pi}{3}\\x=\frac{-4\pi}{3}\end{cases}\)
Seul le deuxième angle appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{\pi}{3}\\x=\frac{2\pi}{3}\end{cases}\)
Question
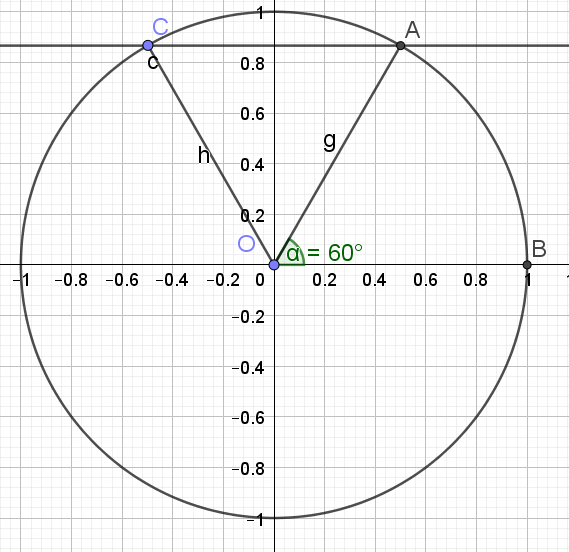
4.\(cos(x)=\frac{\sqrt{3}}{2}\)
Solution
\(cos(x)=\frac{\sqrt{3}}{2}\)
\(cos(x)=cos(\frac{\pi}{6})\)
\(\begin{cases}x=\frac{\pi}{6}+2k\pi\\x=-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\iff \begin{cases}x=\frac{\pi}{6}+2k\pi\\x=-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{\pi}{6}\\x=-\frac{\pi}{6}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{6}+2\pi\\x=-\frac{\pi}{6}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+\frac{12\pi}{6}\\x=-\frac{\pi}{6}+\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{13\pi}{6}\\x=\frac{11\pi}{6}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{6}-2\pi\\x=-\frac{\pi}{6}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{6}-\frac{12\pi}{6}\\x=-\frac{\pi}{6}-\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{-11\pi}{6}\\x=\frac{-13\pi}{6}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{\pi}{6}\\x=-\frac{\pi}{6}\end{cases}\)
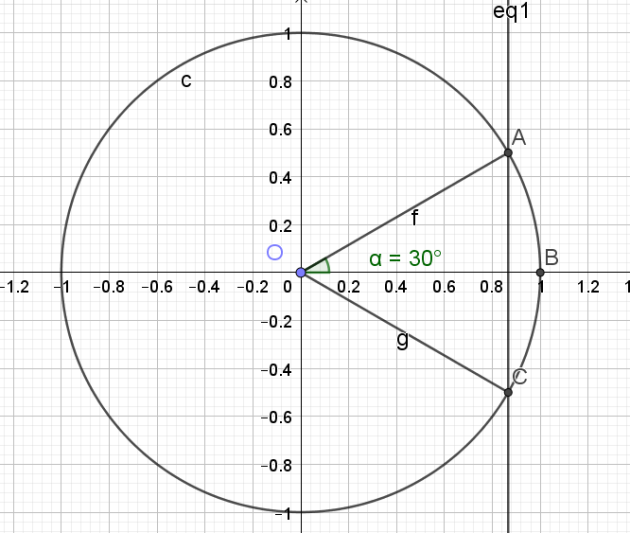
Question
5.\(sin(x)=-\frac{\sqrt{3}}{2}\)
Solution
\(sin(x)=-\frac{\sqrt{3}}{2}\)
\(sin(x)=sin(-\frac{\pi}{3})\)
\(\begin{cases}x=\frac{-\pi}{3}+2k\pi\\x=\pi-\frac{-\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{-\pi}{3}+2k\pi\\x=\frac{3\pi}{3}+\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\iff \begin{cases}x=\frac{-\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{-\pi}{3}\\x=\frac{4\pi}{3}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{-\pi}{3}+2\pi\\x=\frac{4\pi}{3}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{-\pi}{3}+\frac{6\pi}{3}\\x=\frac{4\pi}{3}+\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{5\pi}{3}\\x=\frac{10\pi}{3}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{-\pi}{3}-2\pi\\x=\frac{4\pi}{3}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{-\pi}{3}-\frac{6\pi}{3}\\x=\frac{4\pi}{3}-\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-7\pi}{3}\\x=\frac{-2\pi}{3}\end{cases}\)
Seul le deuxième angle appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus
petites pour la deuxième valeur.
Pour k=-2 :
\(\begin{cases}x=\frac{\pi}{3}-4\pi\\x=\frac{4\pi}{3}-4\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{-\pi}{3}-\frac{12\pi}{3}\\x=\frac{4\pi}{3}-\frac{12\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{-13\pi}{3}\\x=\frac{-8\pi}{3}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{-2\pi}{3}\\x=\frac{-\pi}{3}\\x=\frac{4\pi}{3}\end{cases}\)
or \(\frac{-2\pi}{3}\) et \(\frac{4\pi}{3}\) correspondent au même point sur le cercle
car \(\frac{4\pi}{3}-\frac{-2\pi}{3}=\frac{4\pi}{3}+\frac{2\pi}{3}=\frac{6\pi}{3}=2\pi\)
donc les deux angles sont distincts de un tour.
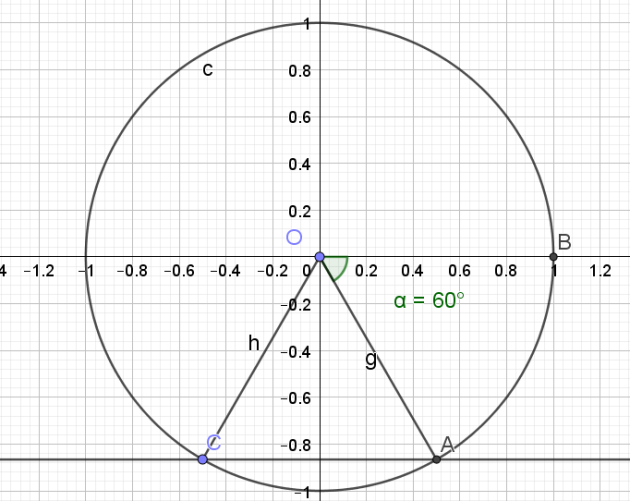
Question
6.\(cos(x)=\frac{\sqrt{2}}{2}\)
Solution
\(cos(x)=\frac{\sqrt{2}}{2}\)
\(cos(x)=cos(\frac{\pi}{4})\)
\(\begin{cases}x=\frac{\pi}{4}+2k\pi\\x=-\frac{\pi}{4}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Dans \(\mathbb{R}\) , les solutions sont :
\(\begin{cases}x=\frac{\pi}{4}+2k\pi\\x=-\frac{\pi}{4}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0:
\(\begin{cases}x=\frac{\pi}{4}\\x=-\frac{\pi}{4}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{4}+2\pi\\x=-\frac{\pi}{4}+2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{4}+\frac{8\pi}{4}\\x=-\frac{\pi}{4}+\frac{8\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\frac{9\pi}{4}\\x=\frac{7\pi}{4}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{4}-2\pi\\x=-\frac{\pi}{4}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{4}-\frac{8\pi}{4}\\x=-\frac{\pi}{4}-\frac{8\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\frac{7\pi}{4}\\x=\frac{-9\pi}{4}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus petites.
Dans l'intervalle des mesures principales, les solutions sont :
\(\begin{cases}x=\frac{\pi}{4}\\x=-\frac{\pi}{4}\end{cases}\)