Exercice : Exercice 16
Question
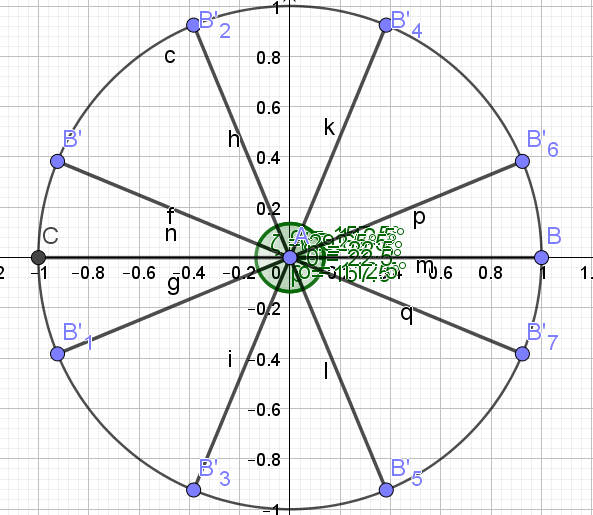
1. Résoudre dans ]-π;π] \(2 cos(3x)=\sqrt{2}\)
Solution
\(cos(3x)=\frac{\sqrt{2}}{2}=cos(\frac{\pi}{4})\)
\(\begin{cases}3x=\frac{\pi}{4}+2k\pi\\3x=-\frac{\pi}{4}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(\mathbb{R}\):
\(\begin{cases}x=\frac{\pi}{12}+\frac{2k\pi}{3}\\x=-\frac{\pi}{12}+\frac{2k\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(]-\pi ;\pi]\):
Pour k=0 :
\(\begin{cases}x=\frac{\pi}{12}\\x=-\frac{\pi}{12}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{12}+\frac{2\pi}{3}\\x=-\frac{\pi}{12}+\frac{2\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{12}+\frac{8\pi}{12}\\x=-\frac{\pi}{12}+\frac{8\pi}{12}\end{cases}\)
\(\iff \begin{cases}x=\frac{9\pi}{12}\\x=\frac{7\pi}{12}\end{cases}\)
Pour k=2 :
\(\begin{cases}x=\frac{\pi}{12}+\frac{4\pi}{3}\\x=-\frac{\pi}{12}+\frac{4\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{12}+\frac{16\pi}{12}\\x=-\frac{\pi}{12}+\frac{16\pi}{12}\end{cases}\)
\(\iff \begin{cases}x=\frac{17\pi}{12}\\x=\frac{15\pi}{12}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{12}-\frac{2\pi}{3}\\x=-\frac{\pi}{12}-\frac{2\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{12}-\frac{8\pi}{12}\\x=-\frac{\pi}{12}-\frac{8\pi}{12}\end{cases}\)
\(\iff \begin{cases}x=\frac{-7\pi}{12}\\x=\frac{-9\pi}{12}\end{cases}\)
Pour k=-2 :
\(\begin{cases}x=\frac{\pi}{12}-\frac{4\pi}{3}\\x=-\frac{\pi}{12}-\frac{4\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{12}-\frac{16\pi}{12}\\x=-\frac{\pi}{12}-\frac{16\pi}{12}\end{cases}\)
\(\iff \begin{cases}x=\frac{-15\pi}{12}\\x=-\frac{17\pi}{12}\end{cases}\)
Ces deux angles n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites.
\(\begin{cases}x=\frac{-9\pi}{12}\\x=\frac{-7\pi}{12}\\x=-\frac{\pi}{12}\\x=\frac{\pi}{12}\\x=\frac{7\pi}{12}\\x=\frac{9\pi}{12}\end{cases}\)
Question
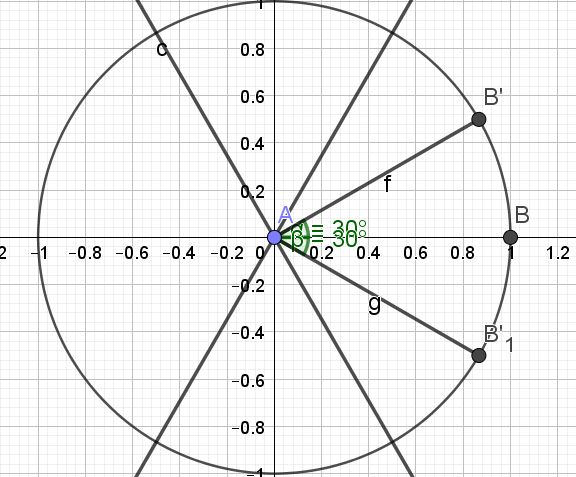
2.Résoudre dans \(\mathbf{R}\) \(sin(x+\frac{\pi}{2})=sin(\frac{\pi}{3})\)
Solution
\(sin(x+\frac{\pi}{2})=sin(\frac{\pi}{3})\)
\(\begin{cases}x+\frac{\pi}{2}=\frac{\pi}{3}+2k\pi\\x+\frac{\pi}{2}=\pi-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{2}+\frac{\pi}{3}+2k\pi\\x=-\frac{\pi}{2}+\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{3\pi}{6}+\frac{2\pi}{6}+2k\pi\\x=-\frac{3\pi}{6}+\frac{4\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Question
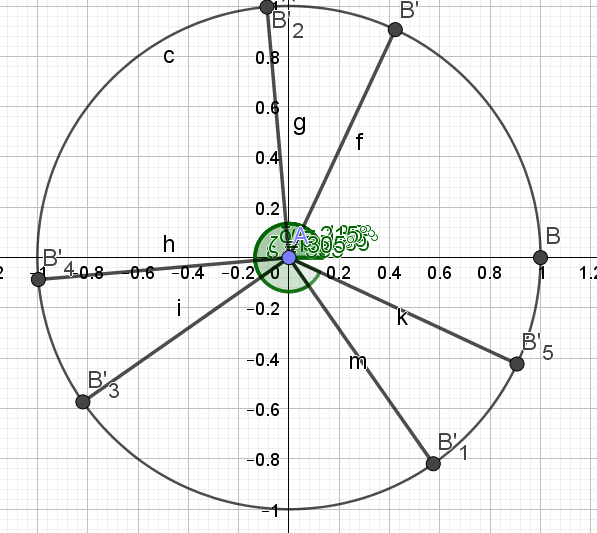
3.Résoudre dans [0;2π[ \(sin(3x+\frac{\pi}{6})=-\frac{\sqrt{2}}{2}\)
Solution
\(sin(3x+\frac{\pi}{6})=-\frac{\sqrt{2}}{2}=sin(-\frac{\pi}{4})\)
\(\iff \begin{cases}3x+\frac{\pi}{6}=-\frac{\pi}{4}+2k\pi\\3x+\frac{\pi}{6}=\pi-(-\frac{\pi}{4})+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}3x=-\frac{\pi}{4}-\frac{\pi}{6}+2k\pi\\3x=\pi+\frac{\pi}{4}-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}3x=-\frac{3\pi}{12}-\frac{2\pi}{12}+2k\pi\\3x=\frac{12\pi}{12}+\frac{3\pi}{12}-\frac{2\pi}{12}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}3x=-\frac{5\pi}{12}+2k\pi\\3x=\frac{13\pi}{12}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{5\pi}{36}+\frac{2k\pi}{3}\\x=\frac{13\pi}{36}+\frac{2k\pi}{3}\end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0 :
\(\begin{cases}x=-\frac{5\pi}{36}\\x=\frac{13\pi}{36}\end{cases}\)
Seule la seconde valeur appartient à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
Inutile de prendre des valeurs plus petites de k pour la première solution.
Pour k=-1 :
\(x=\frac{13\pi}{36}-\frac{2\pi}{3}\)
\(\iff x=\frac{13\pi}{36}-\frac{24\pi}{36}\)
\(\iff x=\frac{-11\pi}{36}\)
Cette valeur n'appartient pas à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
Inutile de prendre des valeurs plus petites de k.
Pour k=1 :
\(\begin{cases}x=-\frac{5\pi}{36}+\frac{2\pi}{3}\\x=\frac{13\pi}{36}+\frac{2\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=-\frac{5\pi}{36}+\frac{24\pi}{36}\\x=\frac{13\pi}{36}+\frac{24\pi}{36}\end{cases}\)
\(\iff \begin{cases}x=\frac{19\pi}{36}\\x=\frac{37\pi}{36}\end{cases}\)
Ces valeurs appartiennent à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
Pour k=2 :
\(\begin{cases}x=-\frac{5\pi}{36}+\frac{4\pi}{3}\\x=\frac{13\pi}{36}+\frac{4\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=-\frac{5\pi}{36}+\frac{48\pi}{36}\\x=\frac{13\pi}{36}+\frac{48\pi}{36}\end{cases}\)
\(\iff \begin{cases}x=\frac{43\pi}{36}\\x=\frac{61\pi}{36}\end{cases}\)
Ces valeurs appartiennent à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
Pour k=3 :
\(\begin{cases}x=-\frac{5\pi}{36}+\frac{6\pi}{3}\\x=\frac{13\pi}{36}+\frac{6\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=-\frac{5\pi}{36}+\frac{72\pi}{36}\\x=\frac{13\pi}{36}+\frac{72\pi}{36}\end{cases}\)
\(\iff \begin{cases}x=\frac{67\pi}{36}\\x=\frac{85\pi}{36}\end{cases}\)
Ces valeurs appartiennent à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
Pour k=4 :
\(\begin{cases}x=-\frac{5\pi}{36}+\frac{8\pi}{3}\\x=\frac{13\pi}{36}+\frac{8\pi}{3}\end{cases}\)
\(\iff \begin{cases}x=-\frac{5\pi}{36}+\frac{96\pi}{36}\\x=\frac{13\pi}{36}+\frac{96\pi}{36}\end{cases}\)
\(\iff \begin{cases}x=\frac{91\pi}{36}\\x=\frac{109\pi}{36}\end{cases}\)
Ces valeurs n'appartiennent pas à [0;2π[\(=[0 ;\frac{72\pi}{36}[\)
\(\begin{cases}x=\frac{13\pi}{36}\\x=\frac{19\pi}{36}\\x=\frac{37\pi}{36}\\x=\frac{43\pi}{36}\\x=\frac{61\pi}{36}\\x=\frac{67\pi}{36}\end{cases}\)
Question
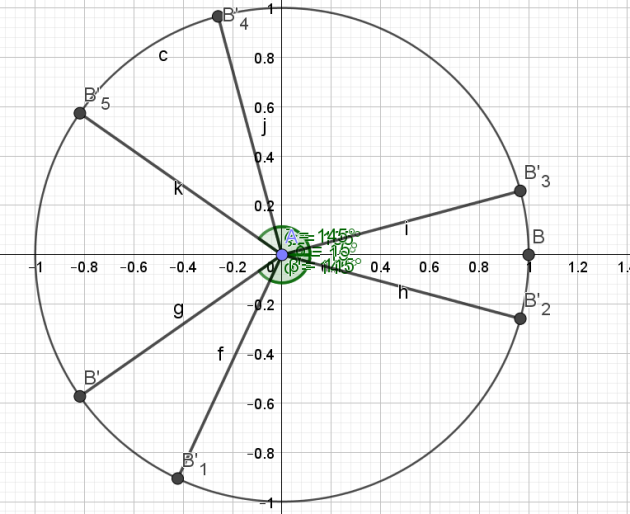
4.Résoudre dans ]-π;π] \(sin(3x)=sin(5x)\)
Solution
\(sin(3x)=sin(5x)\)
\(\begin{cases}3x=5x+2k\pi\\3x=\pi-5x+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}3x=5x+2k\pi\\3x=\pi-5x+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}3x-5x=2k\pi\\3x+5x=\pi+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}-2x=2k\pi\\8x=\pi+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-k\pi\\x=\frac{\pi}{8}+\frac{k\pi}{4}\end{cases}\) \(k\in\mathbb{Z}\)
Solutions dans \(\mathbb{R}\):
\(\iff \begin{cases}x=k\pi\\x=\frac{\pi}{8}+\frac{k\pi}{4}\end{cases}\) \(k\in\mathbb{Z}\)
Solutions dans \(]-π;π] \):
Pour k=0
\(\iff \begin{cases}x=0\\x=\frac{\pi}{8}\end{cases}\)
Pour k=1
\(\begin{cases}x=\pi\\x=\frac{\pi}{8}+\frac{\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\pi\\x=\frac{\pi}{8}+\frac{2\pi}{8}\end{cases}\)
\(\iff \begin{cases}x=\pi\\x=\frac{3\pi}{8}\end{cases}\)
Inutile de prendre des valeurs de k plus grandes pour la première valeur.
Pour k=2
\(x=\frac{\pi}{8}+\frac{2\pi}{4}\)
\(\iff x=\frac{\pi}{8}+\frac{4\pi}{8}\)
\(\iff x=\frac{5\pi}{8}\)
Pour k=3
\(x=\frac{\pi}{8}+\frac{3\pi}{4}\)
\(\iff x=\frac{\pi}{8}+\frac{6\pi}{8}\)
\(\iff x=\frac{7\pi}{8}\)
Pour k=4
\(x=\frac{\pi}{8}+\frac{4\pi}{4}\)
\(\iff x=\frac{\pi}{8}+\frac{8\pi}{8}\)
\(\iff x=\frac{9\pi}{8}\)
Cette valeur n'appartient pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1
\(\begin{cases}x=-\pi\\x=\frac{\pi}{8}-\frac{\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=-\pi\\x=\frac{\pi}{8}-\frac{2\pi}{8}\end{cases}\)
\(\iff \begin{cases}x=-\pi\\x=\frac{-\pi}{8}\end{cases}\)
La première valeur n'appartient pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes pour la première valeur.
Pour k=2
\(x=\frac{\pi}{8}-\frac{2\pi}{4}\)
\(\iff x=\frac{\pi}{8}-\frac{4\pi}{8}\)
\(\iff x=\frac{-3\pi}{8}\)
Pour k=3
\(x=\frac{\pi}{8}-\frac{3\pi}{4}\)
\(\iff x=\frac{\pi}{8}-\frac{6\pi}{8}\)
\(\iff x=\frac{-5\pi}{8}\)
Pour k=4
\(x=\frac{\pi}{8}-\frac{4\pi}{4}\)
\(\iff x=\frac{\pi}{8}-\frac{8\pi}{8}\)
\(\iff x=\frac{-7\pi}{8}\)
Pour k=5
\(x=\frac{\pi}{8}-\frac{5\pi}{4}\)
\(\iff x=\frac{\pi}{8}-\frac{10\pi}{8}\)
\(\iff x=\frac{-9\pi}{8}\)
Cette valeur n'appartient pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Solutions dans \(]-π;π] \):
\(\begin{cases}x=\frac{-7\pi}{8}\\x=\frac{-5\pi}{8}\\ x=\frac{-3\pi}{8}\\x=\frac{-\pi}{8}\\x=0\\x=\frac{\pi}{8}\\x=\frac{3\pi}{8}\\x=\frac{5\pi}{8}\\x=\frac{7\pi}{8}\\x=\pi\end{cases}\)