Exercice : Exercice 5
1.Simplifier chacune des expressions suivantes :
Question
a.\(cos(x-\pi)\)
Solution
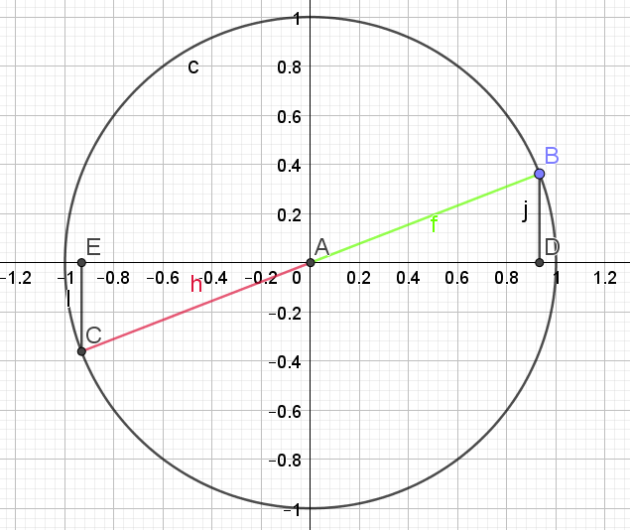
\(cos(x-\pi)=-cos(x)\)
Question
b.\(sin(x-\frac{\pi}{2})\)
Solution
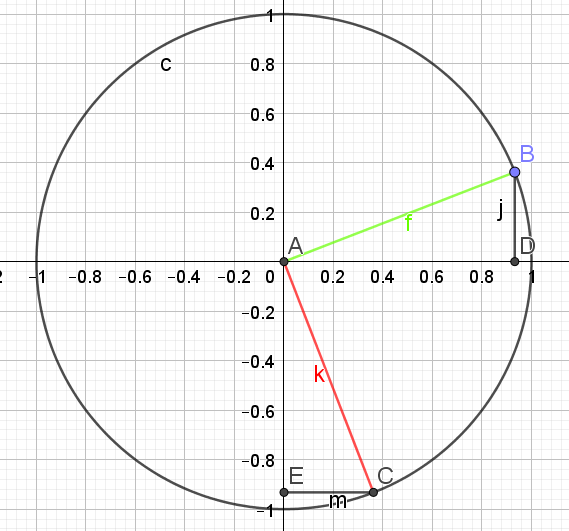
\(sin(x-\frac{\pi}{2})=-cos(x)\)
Question
c.\(sin(x+\frac{\pi}{2})\)
Solution
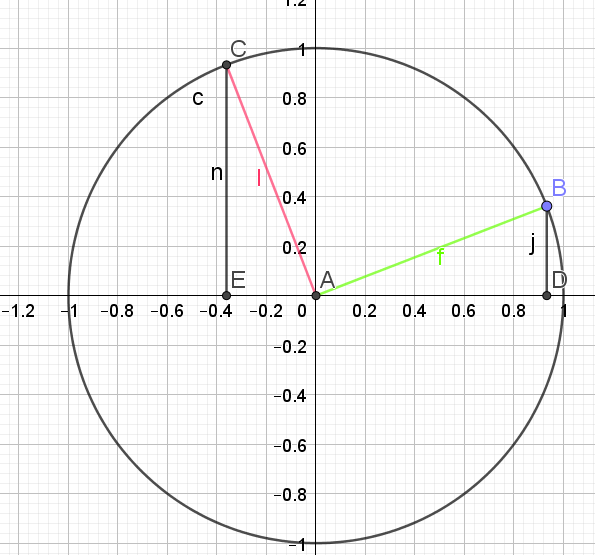
\(sin(x+\frac{\pi}{2})=cos(x)\)
Question
d.\(cos(x+\frac{\pi}{2})\)
Solution

\(cos(x+\frac{\pi}{2})=-sin(x)\)
2.A l'aide de la relation :
\(tan x= \frac{sin x}{cos x}\) où \(x\ne \frac{\pi}{2}+k\pi\)
simplifier les expressions suivantes :
Question
a.\(tan(x+\pi)\)
Solution

\(tan (x+\pi)= \frac{sin(x+\pi)}{cos(x+\pi)}\)
\(sin(x+\pi)=-sin(x)\)
\(sin(x+\pi)=-cos(x)\)
\(\iff tan (x+\pi)= \frac{-sin(x)}{-cos(x)}\)
\(\iff tan (x+\pi)= \frac{sin(x)}{cos(x)}\)
\(\iff tan (x+\pi)= tan(x)\)
Question
b.\(tan(\frac{\pi}{2}-x)\)
Solution
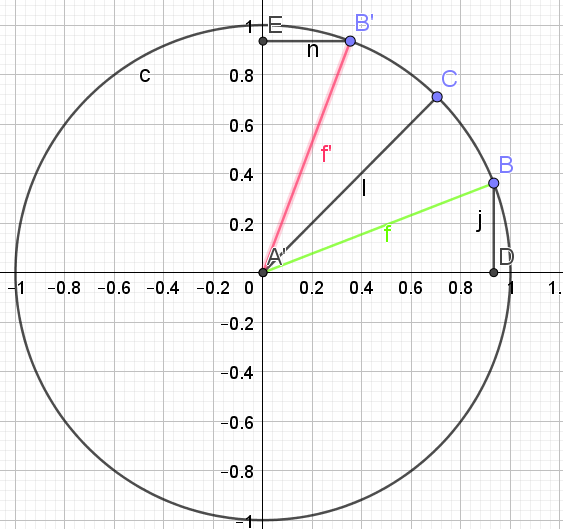
\(tan(\frac{\pi}{2}-x)= \frac{sin(\frac{\pi}{2}-x)}{cos(\frac{\pi}{2}-x)}\)
\(sin(\frac{\pi}{2}-x)=cos(x)\)
\(cos(\frac{\pi}{2}-x)=sin(x)\)
\(\iff tan(\frac{\pi}{2}-x)= \frac{cos(x)}{sin(x)}\)
\(\iff tan(\frac{\pi}{2}-x)=\frac{1}{\frac{sin(x)}{cos(x)}}\)
\(\iff tan(\frac{\pi}{2}-x)= \frac{1}{tan(x)}\)