Exercice : Exercice 6
1.Déterminer les valeurs exactes des expressions ci-dessous :
Question
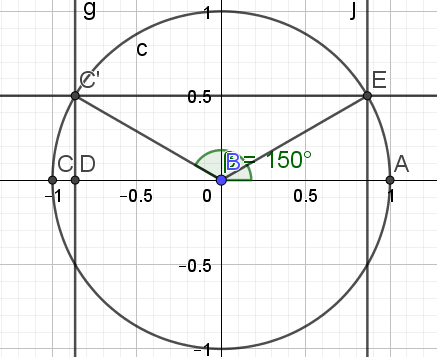
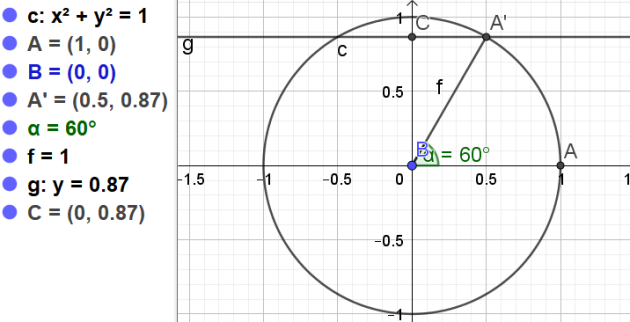
a.\(sin(\frac{7\pi}{3})\)
Solution
\(\frac{7\pi}{3}\notin]-\pi ;\pi]\)
\(\frac{7\pi}{3}=\frac{6\pi}{3}+\frac{\pi}{3}\)
\(\iff \frac{7\pi}{3}=2\pi+\frac{\pi}{3}\)
donc \(\frac{\pi}{3}\) est la mesure principale de \(\frac{7\pi}{3}\)
donc
\(sin(\frac{7\pi}{3})=sin(\frac{\pi}{3}=\frac{\sqrt{3}}{2}\)
Question
b.\(cos(-\frac{5\pi}{4})\)
Solution
\(\frac{-5\pi}{4}\notin]-\pi ;\pi]\)
\(\frac{-\frac{5\pi}{4}}{2\pi}\)
\(= -\frac{5\pi}{4} \times \frac{\pi}{2}\)
\(= -\frac{5}{8}\)
\(-1\le -\frac{5}{8}\le 0\)
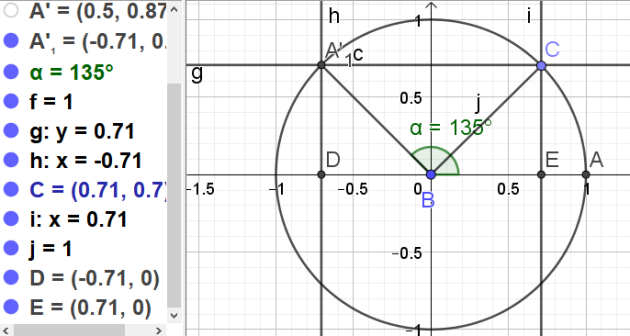
\(-\frac{5\pi}{4}+2\pi=-\frac{5\pi}{4}+\frac{8\pi}{4}=+\frac{3\pi}{4}\)
La mesure principale \(-\frac{5\pi}{4}\) est \(\frac{3\pi}{4}\)
\(cos(\frac{3\pi}{4})=-cos(\frac{\pi}{4})=-\frac{\sqrt{2}}{2}\)
Question
c.\(cos(\frac{5\pi}{6})\)
Solution
\(\frac{5\pi}{6}\in]-\pi ;\pi]\)
\(cos(\frac{5\pi}{6})=-cos(\frac{\pi}{6})=-\frac{\sqrt{3}}{2}\)
