II. Projection orthogonale
Exemple :
Exemple :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Exemple :
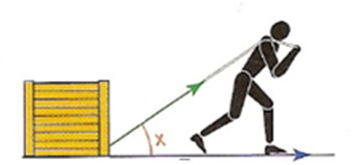
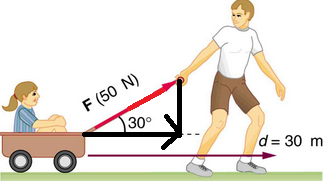
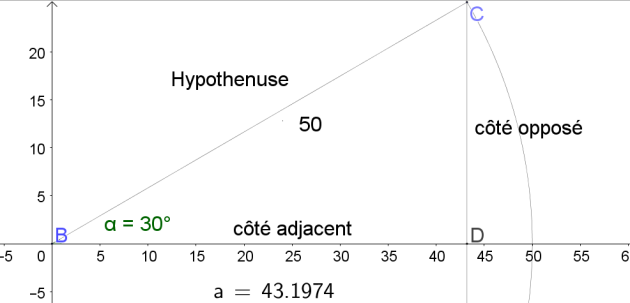
Lorsqu'on tire un objet, ce n'est pas toute la force totale appliquée qui est importante mais uniquement la force projetée sur l'axe horizontal.
Donc par exemple pour la charrette avec la petite fille :
Dans le triangle BDC rectangle en D, on utilise la trigonométrie :
\(cos((\vec{BD}, \vec{BC})=\frac{BD}{BC}\)
\(cos(30°)=\frac{BD}{50}\)
\(donc BD=50 \times cos(30°)\)
La composante horizontale vaut \(F \times cos 30°\)=\(50 \times cos 30°=50 \times \frac{\sqrt{3}}{2}=\frac{50\sqrt{3}}{2}\simeq43,\)
Un des principes du produit scalaire est de projeter un des vecteurs sur la direction d'un second vecteur. Nous regardons la contribution d'un vecteur dans la direction d'un second.
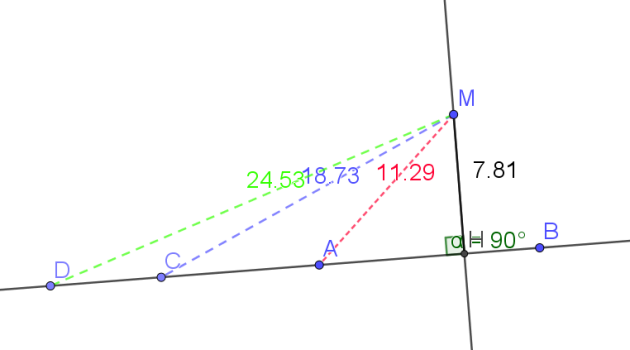
Définition : Construction du projeté orthogonal d'un point sur un segment
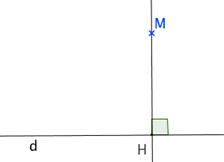
\(\color{red}{\text{Soit une droite d et un point M du plan.}}\)
\(\color{red}{\text{Le projeté orthogonal du point M sur la droite d est le point d'intersection H }}\)
\(\color{red}{\text{de la droite d avec la perpendiculaire à d passant par M :}}\)
La distance MH est la distance minimum entre le point M et la droite (d)
Fondamental : Construction du projeté orthogonal d'un vecteur sur un second vecteur
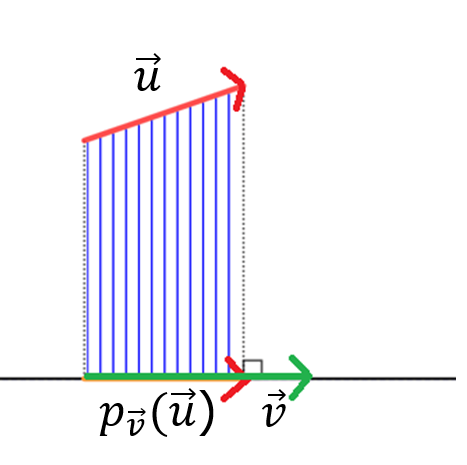
\(p_{\vec{v}}(\vec{u})\) est le projeté orthogonal du vecteur \(\vec{u}\) sur \(\vec{v}\)
Exemple :
1.Quel est le projeté orthogonal du point 𝐷 sur la droite (𝐴𝐶) ?
2.Quel est le projeté orthogonal du segment [𝐴𝐵] sur la droite (𝐴𝐶) ?
Complément :
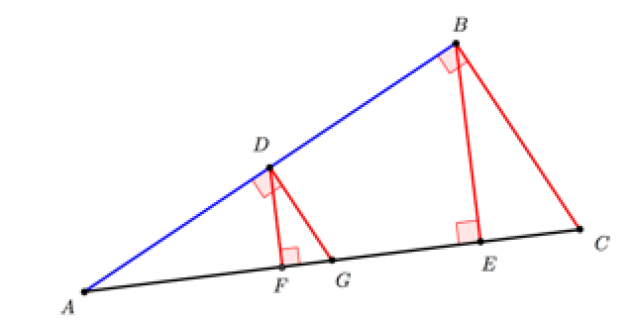
1.Le projeté orthogonal du point 𝐷 sur la droite (𝐴𝐶) est F
2.Le projeté orthogonal du segment [𝐴𝐵] sur la droite (𝐴𝐶) est le segment [AE]
Exemple :
Dans chaque cas, construire les projetés orthogonaux du segment [AB] sur la droite.
Complément :
Exemple :
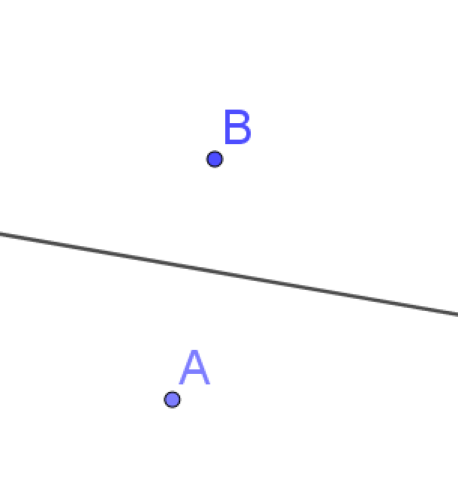
Complément :
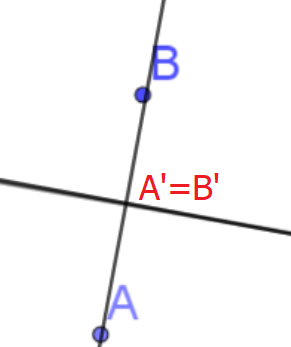
Le projeté orthogonal du segment [AB] sur la droite est réduit au point d'intersection des deux droites.
Exemple :
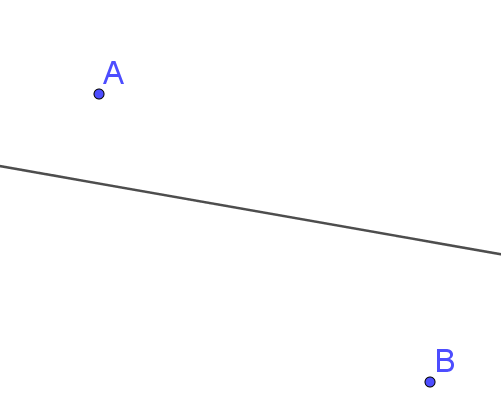
Exemple :
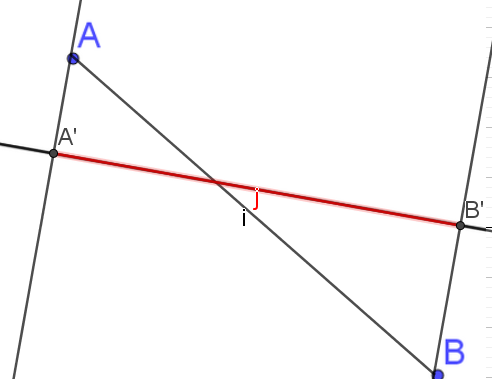
Complément :
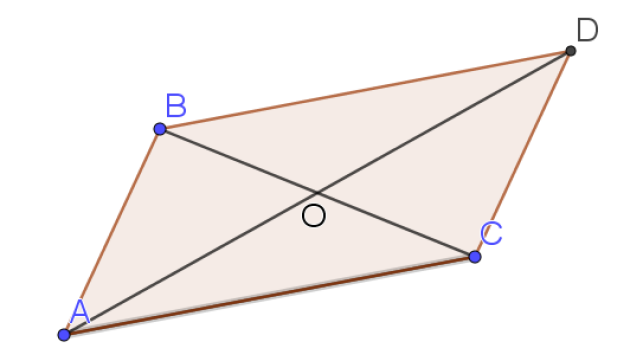
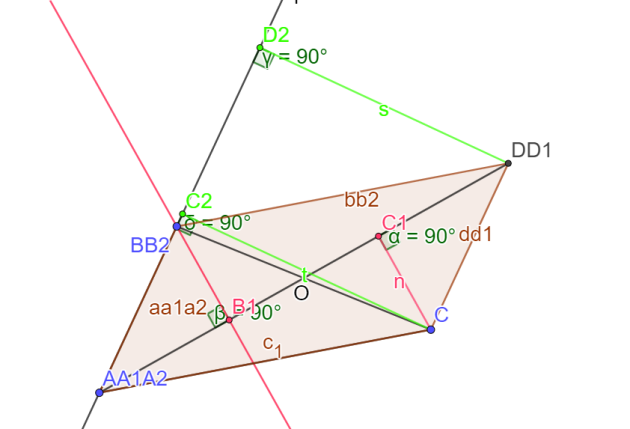
1.Reproduire le parallélogramme ci-contre et tracer les projetés orthogonaux des sommets A,B,C et D :
par la projection orthogonale sur (AD) en rouge :\(A_1,B_1,C_1,D_1\)
2.Que peut on dire du projeté orthogonal d'un point situé sur la droite sur laquelle on projette ?
3. Existe t il d'autres points dont les projections sur (AD) sont \(B_1\)?
4.Tracer en couleur l'ensemble de ces points.
par la projection orthogonale sur (AB) en vert :\(A_2,B_2,C_2,D_2\)
