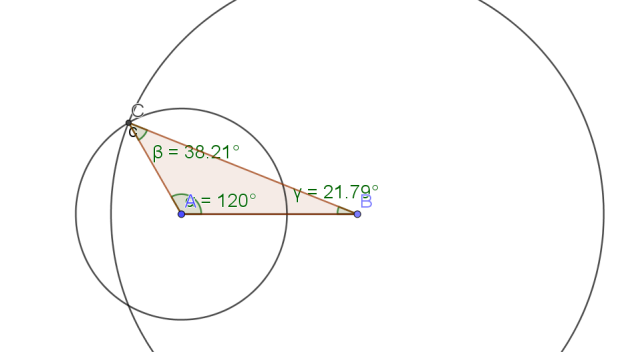
Exercice : Exercice 12 :
On considère le triangle ABC dont les mesures sont : AB= 5; AC= 3 ; BC= 7
Question
Déterminer la mesure, au dixième de degrés près, des angles du triangle ABC
Solution
\(On a : \vec{AB}.\vec{AC}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AC}\|^2-\|\vec{CB}\|^2)\)
donc \(\vec{AB}.\vec{AC}=\frac{1}{2}(5^2+3^2-7^2)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(25+9-49)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(-15)\)
\(\vec{AB}.\vec{AC}=-7,5\)
or \(\vec{AB}.\vec{AC}=\|\vec{AB}\| \times \|\vec{AC}\| \times cos((\vec{AB},\vec{AC}))=5 \times 3 \times cos((\vec{AB},\vec{AC}))\)
d'où \(-7,5=5 \times 3 \times cos((\vec{AB},\vec{AC}))\)
\(-7,5=15 \times cos((\vec{AB},\vec{AC}))\)
\(cos((\vec{AB},\vec{AC}))=\frac{-7,5}{15}=-\frac{1}{2}\)
donc \((\vec{AB},\vec{AC})=\frac{2\pi}{3}\)
donc \(\widehat{BAC}=120°\)
\(On a : \vec{BA}.\vec{BC}=\frac{1}{2}(\|\vec{BA}\|^2+\|\vec{BC}\|^2-\|\vec{CA}\|^2)\)
donc \(\vec{BA}.\vec{BC}=\frac{1}{2}(5^2+7^2-3^2)\)
\(\vec{BA}.\vec{BC}=\frac{1}{2}(25+49-9)\)
\(\vec{BA}.\vec{BC}=\frac{1}{2}(65)\)
\(\vec{BA}.\vec{BC}=32,5\)
or \(\vec{BA}.\vec{BC}=\|\vec{BA}\| \times \|\vec{BC}\| \times cos((\vec{BA},\vec{BC}))=5 \times 7 \times cos((\vec{BA},\vec{BC}))\)
d'où \(32,5=5 \times 7 \times cos((\vec{BA},\vec{BC}))\)
\(32,5=35 \times cos((\vec{BA},\vec{BC}))\)
\(cos((\vec{BA},\vec{BC}))=\frac{32,5}{35}\)
donc \((\vec{BA},\vec{BC})=Arccos(\frac{32,5}{35})\)
donc \(\widehat{ABC}\simeq21,8°\)
\(On a : \vec{CA}.\vec{CB}=\frac{1}{2}(\|\vec{CA}\|^2+\|\vec{CB}\|^2-\|\vec{BA}\|^2)\)
donc \(\vec{CA}.\vec{CB}=\frac{1}{2}(3^2+7^2-3^2)\)
\(\vec{CA}.\vec{CB}=\frac{1}{2}(9+49-25)\)
\(\vec{CA}.\vec{CB}=\frac{1}{2}(33)\)
\(\vec{CA}.\vec{CB}=16,5\)
or \(\vec{CA}.\vec{CB}=\|\vec{CA}\| \times \|\vec{CB}\| \times cos((\vec{CA},\vec{CB}))=3 \times 7 \times cos((\vec{BA},\vec{BC}))\)
d'où \(16,5=21 \times cos((\vec{BA},\vec{BC}))\)
\(cos((\vec{BA},\vec{BC}))=\frac{16,5}{21}\)
donc \((\vec{BA},\vec{BC})=Arccos(\frac{16,5}{21})\)
donc \(\widehat{ABC}\simeq38,2°\)
\(\color{red}{\text{"La somme des mesures des trois angles d'un triangle vaut 180°"}}\)
donc on aurait pu déterminer le troisième angle avec cette propriété :
donc\( \widehat{BAC}+\widehat{ABC}+\widehat{ABC}=180°\simeq120°+21,8°+\widehat{ABC}\)
donc \(\widehat{ABC}\simeq180-120+21,8\simeq38,2°\)