Exercice : Exercice 9 :
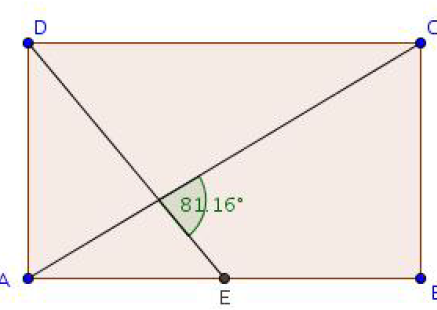
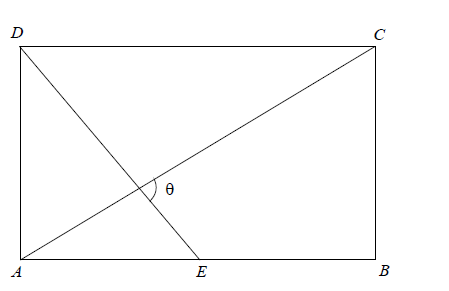
ABCD est un rectangle tel que AD = 3 et AB = 5.
E est le milieu de [AB].
Question
1. Calculer les longueurs AC et DE grâce au théorème de Pythagore.
Solution
Dans le triangle ABC rectangle en B, grâce au théorème de Pythagore :
\(AC^2=AB^2+BC^2\)
\(AC^2=5^2+3^2=25+9=34\)
\(AC=\sqrt{34}\)
Dans le triangle AED rectangle en A, grâce au théorème de Pythagore :
\(DE^2=AD^2+AE^2\)
\(DE^2=3^2+2,5^2=9+6,25=15,25\)
\(DE=\sqrt{15,25}\)
Question
2. Exprimer chacun des vecteurs \(\vec{AC}\) et \(\vec{DE}\) en fonction des deux vecteurs \(\vec{AB}\) et \(\vec{AD}\) ,
Solution
\(\vec{AC}=\vec{AB}+\vec{BC}=\vec{AB}+\vec{AD}\)
car \(\vec{BC}=\vec{AD}\)
\(\vec{DE}=\vec{DA}+\vec{AE}=-\vec{AD}+\frac{1}{2}\vec{AB}\)
donc \(\vec{DE}=-\vec{AD}+\frac{1}{2}\vec{AB}\)
Question
3. Calculer le produit scalaire \(\vec{AC}.\vec{DE}.\)
Solution
\(\vec{AC}.\vec{DE}=(\vec{AB}+\vec{AD}).(-\vec{AD}+\frac{1}{2}\vec{AB})=\vec{AB}.(-\vec{AD})+\vec{AB}.\frac{1}{2}\vec{AB})+\vec{AD}.(-\vec{AD})+\vec{AD}.\frac{1}{2}\vec{AB})\)
\(\vec{AC}.\vec{DE}=\vec{AB}.\frac{1}{2}\vec{AB})+\vec{AD}.(-\vec{AD})\) car les vecteurs \(\vec{AB}\) et \(\vec{AD}\) sont orthgonaux donc \(\vec{AB}.\vec{AD}=\vec{AD}.\vec{AB}=0\)
\(\vec{AC}.\vec{DE}=\frac{1}{2}\vec{AB}^2-\vec{AD}^2\)
\(\vec{AC}.\vec{DE}=\frac{1}{2}AB^2-AD^2\)
\(\vec{AC}.\vec{DE}=\frac{1}{2}\times5^2-3^2\)
\(\vec{AC}.\vec{DE}=\frac{1}{2}\times 25-9\)
\(\vec{AC}.\vec{DE}=12,5-9\)
\(\vec{AC}.\vec{DE}=3,5\)
Question
4. Déduire la valeur de l'angle orienté \(\theta = ( \vec{DE},\vec{AC})\) arrondie à 0,01 degré près.
Solution
\(\vec{AC}.\vec{DE}= \sqrt{34} .\sqrt{15,25} cos(( \vec{DE},\vec{AC}))=3,5\)
\(cos(( \vec{DE},\vec{AC}))=\frac{3,5}{\sqrt{34} .\sqrt{15,25}}\)
\(( \vec{DE},\vec{AC})=Arccos(\frac{3,5}{\sqrt{34} .\sqrt{15,25}})\)
\(( \vec{DE},\vec{AC})\simeq81,16°\)