Exercice : Exercice 13 :
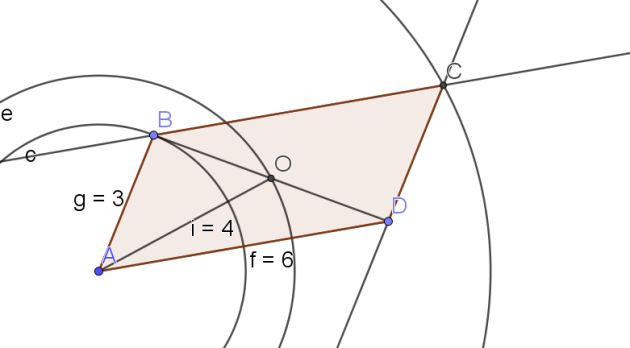
ABCD est un parallélogramme avec AB=3, AD=6 et AC=8
Question
1. Calculer \(\vec{AB}.\vec{AD}\)
Solution
\(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}+\vec{AD}\|^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2)\)
or \(\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AC} |^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2)\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(AC^2-AB^2-AD^2)\)
or d'après l'énoncé \(AB=3, AD=6 \quad et \quad AC=8\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(AC^2-AB^2-AD^2)\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(8^2-3^2-6^2)\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(64-9-36)\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(19)=9,5\)
donc \(\vec{AB}.\vec{AD}=AB.AD.cos((\vec{AB},\vec{AD}))=9,5\)
Question
2. Calculer cos((\(\vec{AB},\vec{AD}\)))
Solution
\(\vec{AB}.\vec{AD}=AB.AD.cos((\vec{AB},\vec{AD}))=9,5\)
\(\iff 3.6.cos((\vec{AB},\vec{AD}))=9,5\)
\(\iff 18.cos((\vec{AB},\vec{AD}))=9,5\)
\(\iff cos((\vec{AB},\vec{AD}))=\frac{9,5}{18}\)
\(\iff cos((\vec{AB},\vec{AD}))=\frac{19}{36}\)
(\vec{AB},\vec{AD})=Arccos(\frac{19}{36})\simeq58,14°
Question
3.Déterminer la mesure de l'angle (\(\vec{AB},\vec{AD}\)) à \(10^{-2}\) près
Solution
\((\vec{AB},\vec{AD})=Arccos(\frac{19}{36})\simeq58,14°\)
Question
4. Calculer en développant \((\vec{AD}-\vec{AB})^2\)
Solution
\((\vec{AD}-\vec{AB})^2=\vec{AD}^2-2\vec{AD}.\vec{AB}+\vec{AB}^2=AD^2-2\vec{AD}.\vec{AB}+AB^2\)
donc \((\vec{AD}-\vec{AB})^2=AD^2-2\vec{AD}.\vec{AB}+AB^2\)
\((\vec{AD}-\vec{AB})^2=6^2-2 \times 9,5+3^2\)
\((\vec{AD}-\vec{AB})^2=36-19 +9\)
\((\vec{AD}-\vec{AB})^2=26\)
Question
5. En déduire la longueur BD.
Solution
\(BD^2=\vec{BD}^2=(\vec{BA}+\vec{AD})^2=(-\vec{AB}+\vec{AD})^2=(\vec{AD}-\vec{AB})^2=26\)
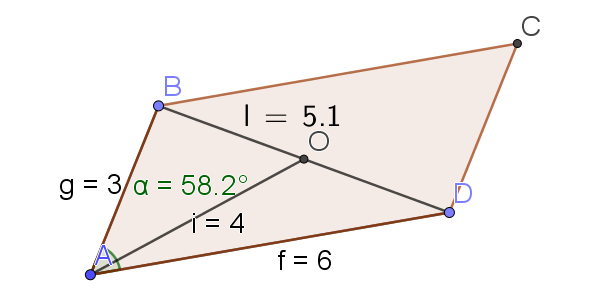
\(BD=\sqrt{26}\simeq5,1\)
Question
6.Faire une figure et vérifier la valeur trouvée de la longueur du segment [BD]