Exercice : Exercice 30 bis :
Question
ABCD est un rectangle, I est le milieu de [AB], J celui de
[CD] ; comment faut-il choisir les dimensions du rectangle ABCD pour que les angles en M et N soient
droits ?
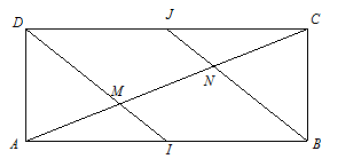
Solution
Pour que l'angle en M soit droit,
il faut que les vecteurs \(\vec{DI}\) et \(\vec{AC}\) soient orthogonaux :
Dans le repère orthonormé \((A ;\frac{\vec{AB}}{||\vec{AB}||},\frac{\vec{AD}}{||\vec{AD}||})\)
les coordonnées des points sont :
A(0 ;0)
B(AB ;0)
D(0 ;AD)
C(AB ;AD)
I(\(\frac{AB}{2} \);0)
\(\vec{AC}=\left ( \begin{array}{c} x_C-x_A\\y_C-y_A \end{array} \right )\)
\(\iff \vec{AC}=\left (\begin{array}{c} AB-0\\AD-0\end{array} \right )\)
\(\iff \vec{AC}=\left (\begin{array}{c} AB\\AD \end{array} \right )\)
\(\vec{DI}=\left (\begin{array}{c} x_I-x_D\\y_I-y_D\end{array} \right )\)
\(\iff \vec{DI}=\left (\begin{array}{c} \frac{AB}{2}-0\\0-AD\end{array} \right )\)
\(\iff \vec{DI}=\left (\begin{array}{c} \frac{AB}{2}\\-AD\end{array} \right )\)
Les vecteurs \(\vec{DI}\) et \(\vec{AC}\) sont orthogonaux
si et seulement si
\(\vec{DI} . \vec{AC}=0\)
\(\iff \frac{AB}{2} \times AB-AD \times AD=0\)
\(\iff \frac{AB^2}{2}-AD^2=0\)
\(\iff AB^2=2AD^2\)
\(\iff AB=\sqrt{2}AD\)