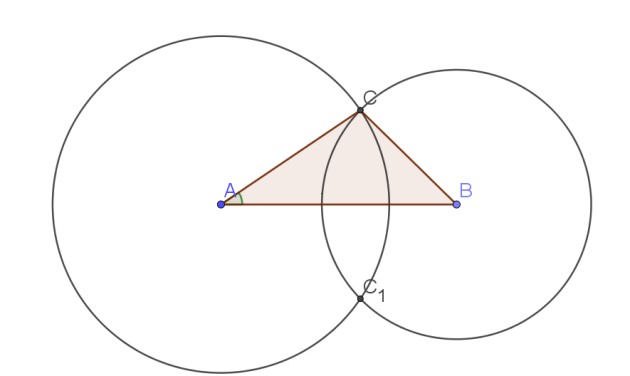
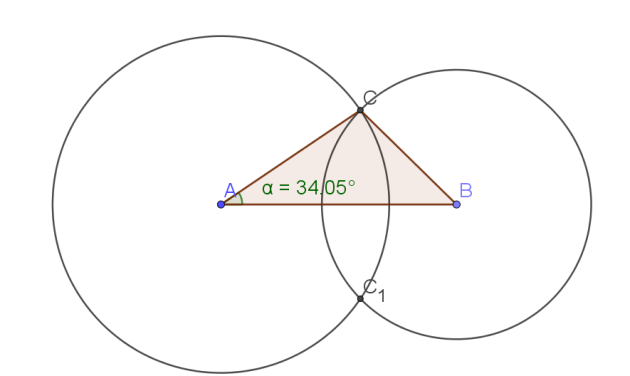
Exercice : Exercice 14 :
On suppose que le triangle ABC est tel que AB = 7, BC = 4 et AC = 5.
Calculer :
Question
a. le produit scalaire \(\vec{AB} ⋅\vec{AC}\)
Solution
\(\vec{AB}.\vec{AC}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AC}\|^2-\|\vec{CB}\|^2)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(AB^2+AC^2-CB^2)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(7^2+5^2-4^2)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(49+25-16)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(74-16)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(58)=29\)
Question
b. la valeur exacte du nombre réel \(cos(\widehat{BAC})\)
Solution
\(\vec{AB}.\vec{AC}=AB.AC.cos((\vec{AB},\vec{AC})=7 \times 5 \times cos((\vec{AB},\vec{AC})=29\)
\(35 \times cos((\vec{AB},\vec{AC})=29\)
\(cos((\vec{AB},\vec{AC})=\frac{29}{35}\)
Question
c. une valeur approchée à\(10^{-2}\) radians près de la mesure de l'angle \(\widehat{BAC}\)
Solution
\(c.\vec{AB},\vec{AC})=Arccos(\frac{29}{35})\simeq34,05°\)
