I.Introduction
Complément :
Exemple : I/Introduction
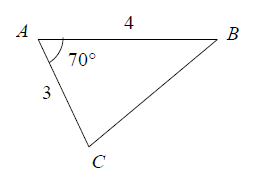
ABC est un triangle tel que AB= 4 AC=3 et (\(\vec{AB}\) ,\(\vec{AC}\))=70°
1.Construire la figure.
2.Mesurer la longueur
3.Calculer la longueur BC, arrondir au dixième.
Complément :
Les méthodes habituelles ne fonctionnent pas :
- pour utiliser le théorème de Pythagore, il manque une longueur et le triangle n'est pas rectangle.
- pour utiliser le théorème de Thalès, il faudrait des droites parallèles.
- pour utiliser la trigonométrie , il faudrait que le triangle est rectangle.
Donc il faudrait un autre outil.... ce sera le but de ce chapitre....


La notion de produit scalaire est apparue pour les besoins de la physique :applications en mécanique et en électromagnétisme .
Le concept relativement récent et a été introduit au milieu du XIXe siècle par le mathématicien allemand Hermann Grassmann (1809-1877), ci-contre.
Il fut baptisé produit scalaire par le mathématicien irlandais William Hamilton (1805-1865) en 1853.
Le produit scalaire permet de :
caractériser l'orthogonalité
d'établir aisément des relations entre les angles ou les longueurs des côtés d'un triangle.
Ces relations connues depuis l'Antiquité au moins, permirent aux astronomes Delambre et Méchain de calculer, à la Révolution française, la mesure d'un arc de méridienne donnant ainsi naissance à une nouvelle unité : le mètre.
