Exercice : Exercice 30 :
Question
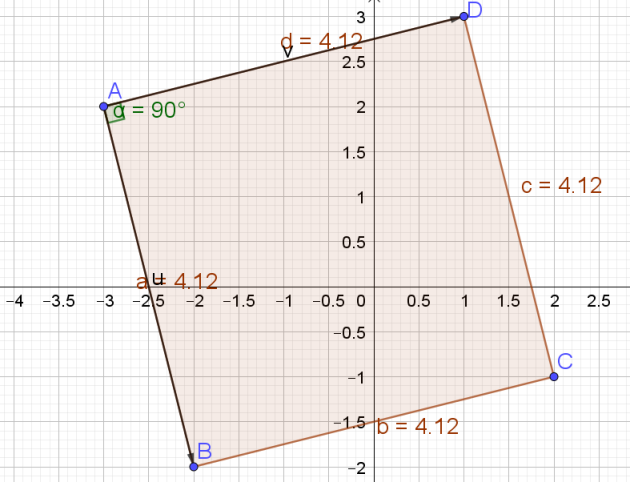
Dans le plan muni d'un repère (O ;I ;J) orthonormé,
on considère les quatre points suivants :
A(-3 ;2) ; B(-2 ;-2) ; C(2 ;-1) ; D(1 ;3)
Question
1.Déterminer la valeur de \(\vec{AB}.\vec{AD}\)
Solution
\(\vec{AB}=\begin{pmatrix}-2-(-3)\\-2-2\end{pmatrix}\)
\(\vec{AB}=\begin{pmatrix}-2+3\\-4\end{pmatrix}\)
\(\vec{AB}=\begin{pmatrix}1\\-4\end{pmatrix}\)
\(\vec{AD}=\begin{pmatrix}1-(-3)\\3-2\end{pmatrix}\)
\(\vec{AD}=\begin{pmatrix}1+3\\1\end{pmatrix}\)
\(\vec{AD}=\begin{pmatrix}4\\1\end{pmatrix}\)
\(\vec{AB}. \vec{AD}=1 \times 4 +(-4) \times 1=4-4=0\)
donc les vecteurs \(\vec{AB}\) et \(\vec{AD}\) sont orthogonaux donc \(\color{magenta}{\textbf{les droites (AB) et (AD) sont perpendiculaires.}}\)
Question
2.Démontrer que le quadrilatère ABCD est rectangle.
Solution
\(\vec{BC}=\begin{pmatrix}2-(-2)\\(-1)-(-2)\end{pmatrix}\)
\(\vec{BC}=\begin{pmatrix}2+2\\-1+2\end{pmatrix}\)
\(\vec{BC}=\begin{pmatrix}4\\1\end{pmatrix}\)
On a donc \(\vec{AD}=\vec{BC}\) or si deux côtés d'un quadrilatère forment des vecteurs égaux, on peut en déduire que le quadrilatère est un parallélogramme.
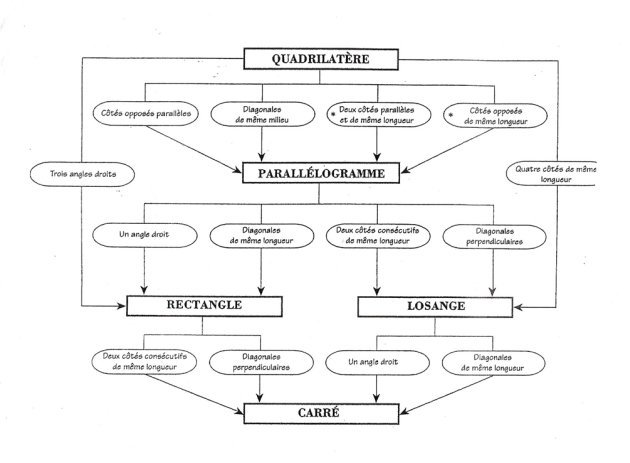
Comme (AB) et (AD) sont perpendiculaires, on en déduit que le quadrilatère est un parallélogramme ayant un angle droit donc \(\color{magenta}{\textbf{il s'agit d'un rectangle }}\)d'après le diagramme des propriétés ci-dessous.
Question
3.Démontrer que le quadrilatère ABCD est un carré.
Solution
Pour montrer que le quadrilatère ABCD est un carré, on peut montrer que deux côtés consécutifs sont de même longueur.
\(\|\vec{AB}\|=\sqrt{1^2+(-4)^2}=\sqrt{1+16}=\sqrt{17}\)
\(\|\vec{AD}\|=\sqrt{4^2+1^2}=\sqrt{16+1}=\sqrt{17}\)
donc les deux côtés consécutifs [AB] et [AD] sont de même longueur, on en déduit que le quadrilatère \(\color{magenta}{\textbf{ABCD est un carré. }}\)