Exercice : Exercice 6 :
Déterminer les produits scalaires des vecteurs \(\vec{AB}\) et \(\vec{AC}\) :
Question
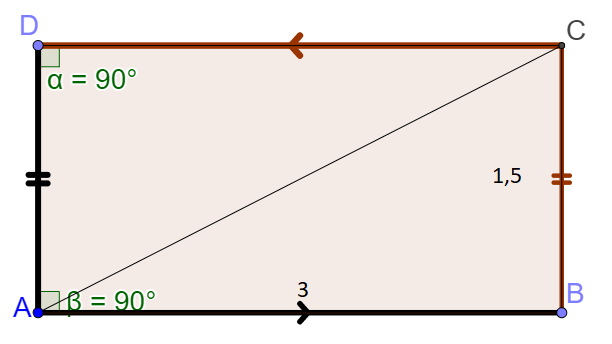
Solution
\(\vec{AB}.\vec{AC}= 3 \times 3 =\color{red}{9} \)car \(\vec{AC}\) se projette orthogonalement en \(\vec{AB}\) sur \(\vec{AB}\)
Question

Solution
\(\vec{AB}.\vec{AC}=3 \times 2 \times cos(\pi)=6 \times (-1)=\color{red}{-6}\)
Question
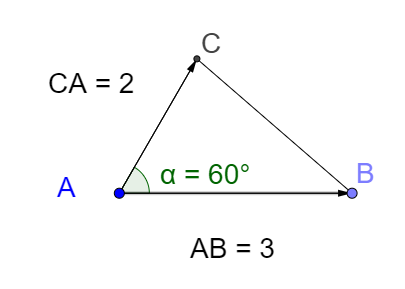
Solution
\(\vec{AB}.\vec{AC}=3 \times 2 \times cos(\frac{\pi}{3})=3 \times 2 \times \frac{1}{2}=\color{red}{3}\)
Question
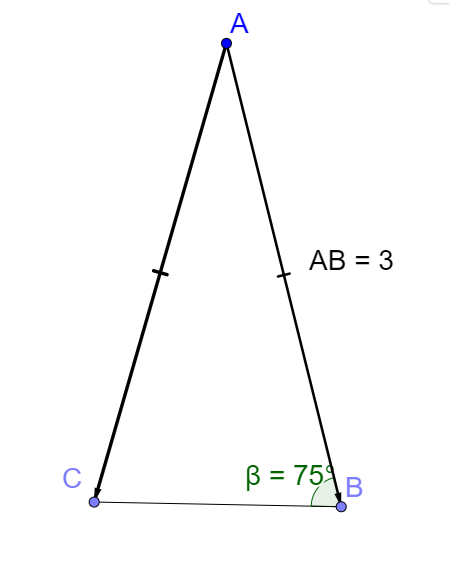
Solution
\(\vec{AB}.\vec{AC}=3 \times 3 \times cos(180-2\times 75)=9 \times cos(30°)=9 \times cos(\frac{\pi}{6})=9 \times \frac{\sqrt{3}}{2}=\color{red}{4,5\sqrt{3}}\)
Question
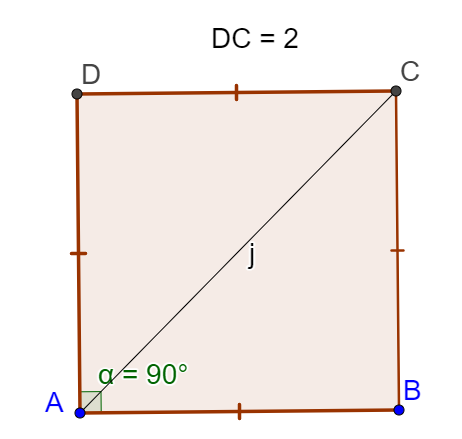
Solution
\(\vec{AB}.\vec{AC}=2 \times 2 =\color{red}{4} \)car \(\vec{AC}\) se projette orthogonalement en \(\vec{AB}\) sur \(\vec{AB}\)