VII. Vecteurs orthogonaux
Exemple :
\(\color{magenta}{\text{Exercices 30 à 32}}\)
Définition :
\(\color{red}{\textbf{On dit que deux vecteurs non nuls }} \vec{u} \quad et \quad \vec{v} \quad \color{red}{\textbf{ sont orthogonaux lorsqu'ils forment un angle droit}}\)
\(\color{red}{\textbf{C'est-à-dire lorsque } \quad \color{red}{(\vec{u};\vec{v})=\frac{\pi}{2}+2k\pi} }\)
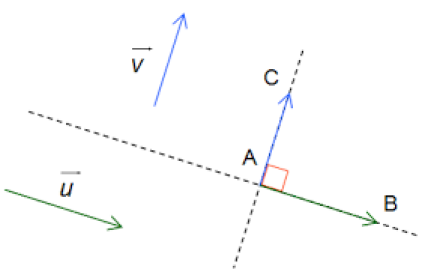
\(\color{red}{ \quad ou \quad (\vec{u};\vec{v})=\frac{-\pi}{2}+2k\pi}\)
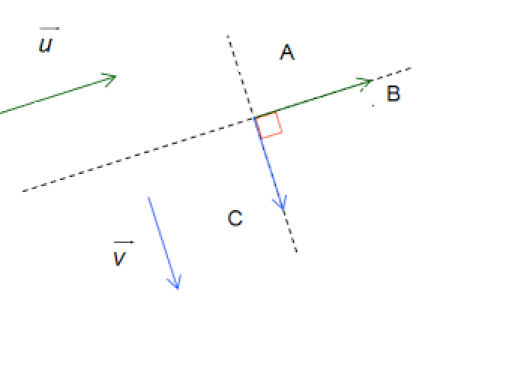
Remarque :
\(\color{magenta}{\textbf{Par convention le vecteur nul est orthogonal à tous les vecteurs.}}\)
Fondamental :
\(\color{red}{\textbf{Les vecteurs } \vec{u} \textbf{ et } \vec{v} \textbf{ et sont orthogonaux si et seulement si : } \vec{u}.\vec{v}=0.}\)
Complément : Démonstration
Si l'un des vecteurs est nul, la démonstration est évidente.
Supposons le contraire : les deux vecteurs ne sont pas nuls.
\(\vec{u}\).\(\vec{v}\)=0.
⟺\(\|\vec{u}\|\|\vec{v}\| cos(\vec{u};\vec{v})=0\)
⟺ cos(\(\vec{u}\);\(\vec{v}\))=0
⟺Les vecteurs \(\vec{u}\) et \(\vec{v}\)sont orthogonaux
Rappel :
\(\color{red}{\textbf{ Un coefficient directeur de la droite d'équation y=ax+b est } \vec{u}=\begin{pmatrix}1\\a\end{pmatrix}}\)
Exemple :
\(\color{magenta}{\text{Exercices 33}}\)
Fondamental :
\(\color{red}{\textbf{Les vecteurs non nuls de coordonnées (1 ; m) et (1 ; m') sont respectivement, des vecteurs directeurs des droites (d) et (d').}}\)
\(\color{red}{\textbf{Ils sont orthogonaux, et (d) et (d') sont perpendiculaires, si, et seulement si : 1 + mm' = 0:}}\)
VI Vecteur normal à une droite
Exemple :
\(\color{magenta}{\text{Exercices 34}}\)
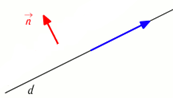
Définition :
\(\color{red}{\textbf{On appelle vecteur normal à une droite (d), tout vecteur } \vec{n} \textbf{ non nul orthogonal à un vecteur directeur de (d)}}\)
Fondamental :
Le plan est muni d'un repère \((O;\vec{i} ;\vec{j})\) orthonormal.
\(\color{red}{ \textbf{Soit A un point du plan et }\vec{n}(a,b) \textbf{ un vecteur non nul.}}\)
\(\color{red}{\textbf{ L'ensemble des points M tels que }\vec{AM}.\vec{n}=0 \textbf{ est la droite passant par A et admettant } \vec{n} \textbf{ pour vecteur normal.}}\)
\(\color{red}{\textbf{ Elle admet pour équation }ax+by+c=0}\)
Fondamental :
Le plan est muni d'un repère \((O;\vec{i} ;\vec{j})\) orthonormal.
Toute droite admettant une équation de la forme \(ax +by +c\) = 0 admet \(\vec{n} = (a ; b)\) comme vecteur normal.
Fondamental : Distance d'un point à une droite
Le plan est muni d'un repère \((O;\vec{i} ;\vec{j})\) orthonormal.
Soit \(\mathbb{D}\) une droite d'équation :
\(ax +by +c = 0\) et A(α; β) un point quelconque du plan.
La distance de A à \(\mathbb{D}\),
notée d(A,\(\mathbb{D}\)) est
d(A,\(\mathbb{D}\)) = \(\frac{|aα+bβ+c|}{\sqrt{a^2 +b^2}}\)
Complément : Démonstration
\(|\vec{AH}.\vec{n}|=AH.||\vec{n}||.cos(\vec{AH},\vec{n})\)
\(\iff |\vec{AH}.\vec{n}|=AH.||\vec{n}||.cos(0)\)
\(\iff |\vec{AH}.\vec{n}|=AH.||\vec{n}||\)
\(|\vec{AH}.\vec{n}|=|\left(\begin{array}{c}x_H-x_A\\y_H-x_A\end{array}\right).\left(\begin{array}{c}a\\b\end{array}\right)|=AH.||\vec{n}||\)
\(\iff |\left(\begin{array}{c}x_H-\alpha\\y_H-\beta\end{array}\right).\left(\begin{array}{c}a\\b\end{array}\right)|=AH.||\vec{n}||\)
\(\iff |a(x_H-\alpha)+b(y_H-\beta)|=AH.\sqrt{a^2+b^2}\)
\(\iff AH=\frac{|a(x_H-\alpha)+b(y_H-\beta)|}{\sqrt{a^2+b^2}}\)
\(\iff AH=\frac{|ax_H-a\alpha+by_H-b\beta|}{\sqrt{a^2+b^2}}\)
\(\iff AH=\frac{|ax_H+by_H-a\alpha-b\beta|}{\sqrt{a^2+b^2}}\)
Le point H appartient à la droite d'équation \(ax+by+c=0\)
donc \(ax_H+by_H+c=0\)
donc \(ax_H+by_H=-c\)
\(\iff AH=\frac{|-c-a\alpha-b\beta|}{\sqrt{a^2+b^2}}\)
\(\iff AH=\frac{|-a\alpha-b\beta-c|}{\sqrt{a^2+b^2}}\)
\(\iff AH=\frac{|a\alpha+b\beta+c|}{\sqrt{a^2+b^2}}\)
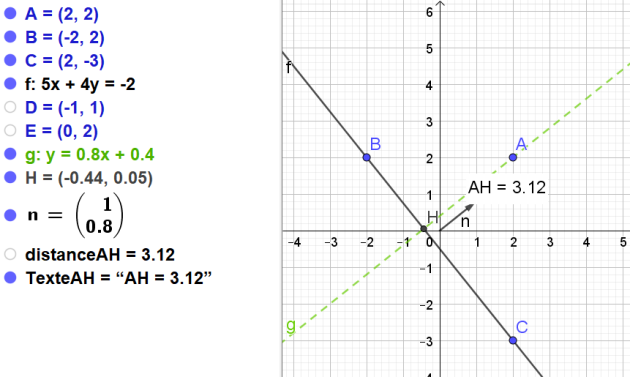
Exemple :
Calculer la distance du point A(2 ;2) à la droite d'équation \(5x+4y+2=0\)
\(AH=\frac{|a\alpha+b\beta+c|}{\sqrt{a^2+b^2}}\)
\(\vec{n}=\left( \begin{array}{c} 5\\ 4 \end{array} \right )\)
\(AH=\frac{|5 \times 2 +4 \times 2+2|}{\sqrt{5^2+4^2}}\)
\(\iff AH=\frac{|10 +8+2|}{\sqrt{25+16}}\)
\(\iff AH=\frac{20}{\sqrt{41}}\)