Exercice : Exercice 15 :
Le plan est rapporté à un repère orthonormé (O ;\(\vec{i} ;\vec{j}\)).
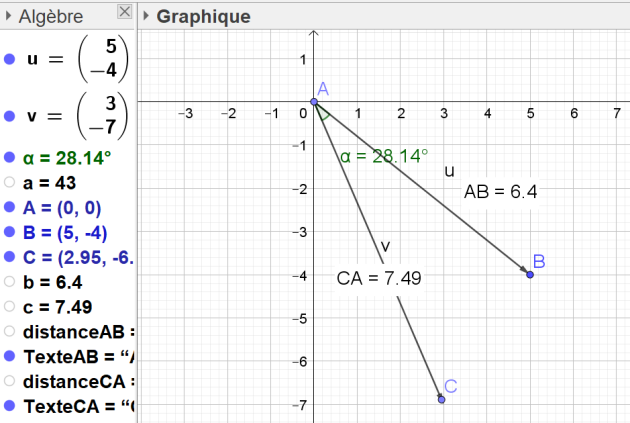
Soit \(\vec{u}\)(5 ;-4) et \(\vec{v}\)(3,-7)
Calculer :
Question
1. le produit scalaire\(\vec{u}.\vec{v}\)
Question
2. l'angle que font les vecteurs \(\vec{u}\) et \(\vec{v}\)\(\)\(\)
Solution
\(\vec{u}.\vec{v}=\|\vec{u}\|.\|\vec{v}\|.cos(\vec{u},\vec{v})\)
\(\|\vec{u}\|=\sqrt{5^2+(-4)^2}=\sqrt{25+16}=\sqrt{41}\)
\(\|\vec{v}\|=\sqrt{3^2+(-7)^2}=\sqrt{9+49}=\sqrt{58}\)
\(\vec{u}.\vec{v}=\sqrt{41}.\sqrt{58}.cos(\vec{u},\vec{v})=43\)
\(cos(\vec{u},\vec{v})=\frac{43}{\sqrt{41}.\sqrt{58}}\)
\((\vec{u},\vec{v})\)=Arccos(\(\frac{43}{\sqrt{41}.\sqrt{58}} \simeq Arccos(0,88)\simeq28,14°\)
L'angle des vecteurs \(\vec{u}\) et \(\vec{v}\) est donc de environ 28,14°