Exercice : Exercice 10 :
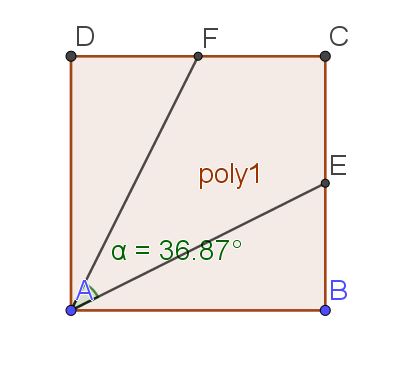
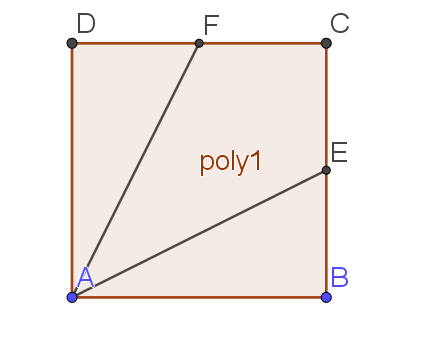
Soit ABCD un carré de côté 4.E le milieu de [BC] et F celui de [DC].
On se propose d'évaluer l'angle \(\widehat{FAE}\).
Question
1.Ecrire les vecteurs \(\vec{AE}\) et \(\vec{AF}\) en fonction des vecteurs \(\vec{AB}\) et \(\vec{AD}\) grâce à la relation de Chasles.
Solution
\(\vec{AE}=\vec{AB}+\vec{BE}=\vec{AB}+\frac{1}{2}\vec{BE}=\vec{AB}+\frac{1}{2}\vec{AD}\)
\(\vec{AF}=\vec{AD}+\vec{DF}=\vec{AD}+\frac{1}{2}\vec{DC}=\vec{AD}+\frac{1}{2}\vec{AB}=\frac{1}{2}\vec{AB}+\vec{AD}\)
Question
2.A l'aide des relations de l'exercice 1, montrer que \(\vec{AE}.\vec{AF}=4^2=16\)
Solution
\(\vec{AE}.\vec{AF}=(\vec{AB}+\frac{1}{2}\vec{AD})(\vec{AD}+\frac{1}{2}\vec{AB})=\vec{AB}.\vec{AD}+\vec{AB}.\frac{1}{2}\vec{AB}+\frac{1}{2}\vec{AD}.\vec{AD}+\frac{1}{2}\vec{AD}.\frac{1}{2}\vec{AB}\)
\(\begin{cases}\vec{AB}.\vec{AD}=0 \textbf{car les vecteurs }\vec{AB} \quad et \quad \vec{AD} \textbf{ sont orthogonaux }\\ \vec{AB}.\frac{1}{2}\vec{AB}=\frac{1}{2}\vec{AB}^2=\frac{1}{2}AB^2=\frac{1}{2}\times 4^2=\frac{1}{2}\times 16=8\\ \frac{1}{2}\vec{AD}.\vec{AD}=\frac{1}{2}\vec{AD}^2=\frac{1}{2}AD^2=\frac{1}{2}\times 4^2=\frac{1}{2}\times 16=8\\\frac{1}{2}\vec{AD}.\frac{1}{2}\vec{AB}=0 \textbf{car les vecteurs }\vec{AB} \quad et \quad \vec{AD} \textbf{ sont orthogonaux }\end{cases}\)
donc \(\vec{AE}.\vec{AF}=8+8=16\)
Question
3. Dérerminer les longueurs AF et AE grâce au théorème de Pythagore.
Solution
Dans le triangle ADF rectange en D, j'utilise le théorème de Pythagore :
AF=\(\sqrt{AD^2+DF^2}\)
AF=\(\sqrt{4^2+2^2}\)
AF=\(\sqrt{16+4}=\sqrt{20}\)
Dans le triangle ABE rectange en B, j'utilise le théorème de Pythagore :
AE=\(\sqrt{AB^2+BE^2}\)
AE=\(\sqrt{4^2+2^2}\)
AE=\(\sqrt{16+4}=\sqrt{20}\)
Question
4.En déduire une valeur exacte de \(cos((\vec{AF},\vec{AE}))\)
Solution
\(\vec{AE}.\vec{AF}=\|\vec{AE}\|times\|\vec{AE}\|\times cos((\vec{AF},\vec{AE}))=\sqrt{20}\times \sqrt{20} \times cos((\vec{AF},\vec{AE}))=20 \times cos((\vec{AF},\vec{AE}))=16\)
donc \(cos((\vec{AF},\vec{AE}))=\frac{16}{20}=\frac{4}{5}=0,8\)
Question
5.En déduire une valeur arrondie à \(10^{-1}\) de l'angle \((\vec{AF},\vec{AE})\)
Solution
Donc \((\vec{AF},\vec{AE})=Arccos(0,8)\simeq36,9°\)