Exercice : Exercice 37 :
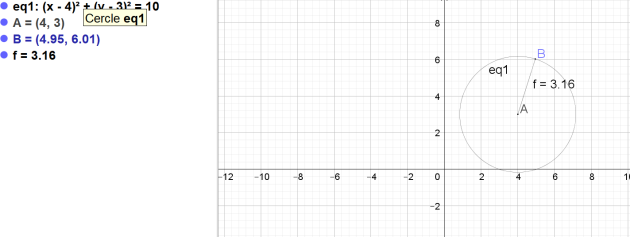
On considère l'ensemble des points \(M (x ; y)\) du plan muni d'un repère orthonormal tels que : \((x - 4)^2 + (y - 3)^2 = 10.\)
Question
Pourquoi l'ensemble des points est-il un cercle ?
Quelles sont les coordonnées du centre de ce cercle ?
Solution
\((x - 4)^2 + (y - 3)^2 = 10\)
\(\Leftrightarrow \sqrt{(x - 4)^2 + (y - 3)^2} = \sqrt{10}\)
\(\Leftrightarrow AM = \sqrt{10}\) où A est le point de coordonnées (4 ;3)
donc l'ensemble des points est le cercle de centre A(4 ;3) et de rayon \(\sqrt{10}\simeq3,16\)
