Exercice : Exercice 11 :
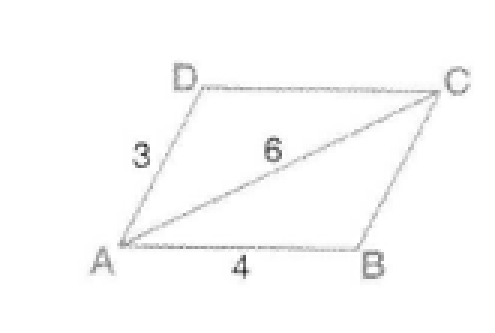
Question
1.Calculer le produit scalaire des vecteurs \(\vec{AB}\) et \(\vec{AC}\)
Solution
On ne connait (et on ne peut pas calculer) l'angle des vecteurs \(\vec{AB}\) et \(\vec{AC}\)
on utilise donc la formule :
\(\vec{AB}.\vec{AC}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AC}\|^2-\|\vec{BC}\|^2)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2}(4^2+6^2-3^2)\) car BC=AD
\(\vec{AB}.\vec{AC}=\frac{1}{2}(16+36-9)\)
\(\vec{AB}.\vec{AC}=\frac{1}{2} \times (43)\)
\(\vec{AB}.\vec{AC}=21,5\)
Question
2. Calculer une valeur exacte de \(cos((\vec{AB},\vec{AC}))\)
Solution
\(\vec{AB}.\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})=4 \times 6 \times cos(\vec{AB},\vec{AC})\)
d'où
\(24 \times cos(\vec{AB},\vec{AC})=21,5\)
donc
\(cos(\vec{AB},\vec{AC})=\frac{21,5}{24}\)
\(cos(\vec{AB},\vec{AC})=\frac{43}{48}\)
Question
3. En déduire une valeur arrondie à \(10^{-2}\) de la mesure de l'angle \((\vec{AB},\vec{AC})\)
Solution
\((\vec{AB},\vec{AC})=Arccos(\frac{43}{48})\simeq26,38°\)