Exercice : Exercice 4 :
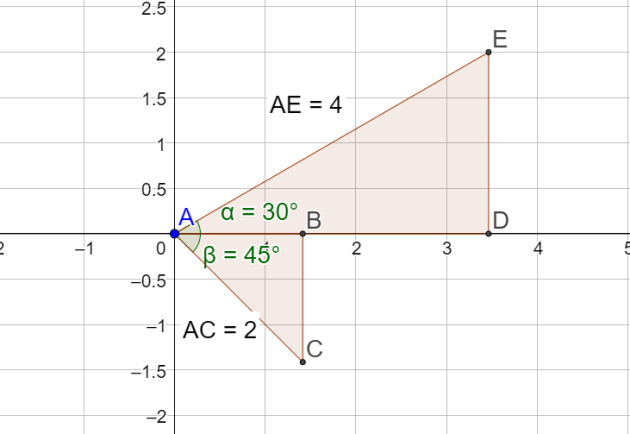
On considère la figure ci-dessous où AE=4cm et AC=2cm
1.On considère le repère orthonormé, orienté dans le sens direct, dont l'unité mesure 1cm,
et dont l'axe des abscisses est la droite (AD).
Question
a.Montrer que \(E(2\sqrt{3} ;2)\)
Solution
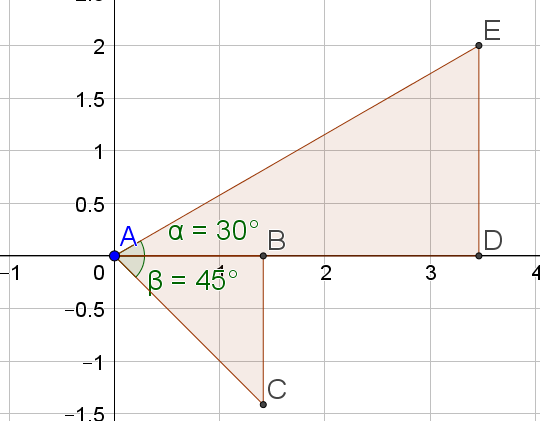
.Dans le triangle ADE rectangle en D :
\(cos(\widehat{EAD})=\frac{AD}{AE}=\frac{AD}{4}\)
\(cos(\frac{\pi}{4})=\frac{AD}{4}\)
\(AD= 4 \times cos(\frac{\pi}{6})=4 \times \frac{\sqrt{3}}{2}=2\sqrt{3}\)
donc \(x_E=2\sqrt{3}\)
Dans le triangle ADE rectangle en D :
\(sin(\widehat{EAD})=\frac{DE}{AE}=\frac{DE}{4}\)
\(sin(\frac{\pi}{6})=\frac{DE}{4}\)
\(DE= 4 \times sin(\frac{\pi}{6})=4 \times \frac{1}{2}=2\)
donc \(y_E=2\)
Question
b.Déterminer les coordonnées des autres points de cette figure.
Solution
A(0,0)
Dans le triangle ABC rectangle en B :
\(cos(\widehat{BAC})=\frac{AB}{AC}=\frac{AB}{2}\)
\(cos(\frac{\pi}{4})=\frac{AB}{2}\)
\(AB= 2 \times cos(\frac{\pi}{4})=2\times \frac{\sqrt{2}}{2}=\sqrt{2}\)
donc \(x_C=\sqrt{2}\)
Dans le triangle ADE rectangle en D :
\(sin(\widehat{BAC})=\frac{BC}{AC}=\frac{BC}{2}\)
\(sin(\frac{\pi}{4})=\frac{BC}{2}\)
\(BC= 2 \times sin(\frac{\pi}{4})=2 \times \frac{\sqrt{2}}{2}=\sqrt{2}\)
donc \(y_C=-\sqrt{2}\)
\(C(\sqrt{2} ,-\sqrt{2})\)
\(B(2\sqrt{2} , 0)\)
\(D(2\sqrt{3} ,0)\)
\(E(2\sqrt{3} ,2)\)
2.Déterminer la valeur des produits scalaires ci-dessous :
Question
\(a. \vec{AB}.\vec{AD}\)
Solution
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(\sqrt{2} )^2+(0-0)^2}=\sqrt{(\sqrt{2} )^2}=\sqrt{2} \)
\(AD=\sqrt{(x_D-x_A)^2+(y_D-y_A)^2}=\sqrt{(2\sqrt{3} )^2+(0-0)^2}=\sqrt{(2\sqrt{3} )^2}=2\sqrt{3} \)
\(\vec{AB}\vec{AD}=\|\vec{AB}\|\times\|\vec{AB}\| \times cos((\vec{AB},\vec{AD}))\)
\(\vec{AB}\vec{AD}= \sqrt{2} \times 2\sqrt{3} \times cos(0)=2\sqrt{6}\)
Question
\(b.\vec{AB}.\vec{AE}\)
Solution
\(\vec{AB}\vec{AE}=\|\vec{AB}\|\times\|\vec{AE}\| \times cos((\vec{AB},\vec{AE}))=\vec{AB}\vec{AD}=2\sqrt{6}\)
Question
\(c.\vec{AC}.\vec{AD}\)
Solution
\(\vec{AC}\vec{AD}=\vec{AB}\vec{AD}=2\sqrt{6}\)