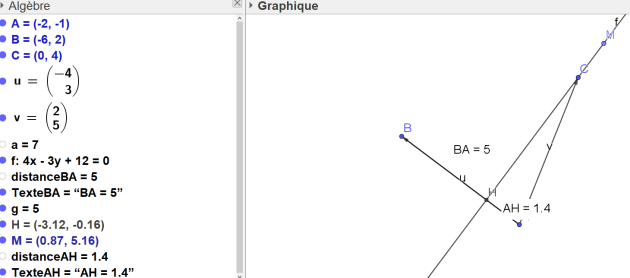
Exercice : Exercice 18 :
Le plan étant muni d'un repère orthonormé, on considère les points A( -2;-1 ) ,B( -6;2 ) et C( 0;4 ) .
Question
1. Faire une figure
Question
2. Calculer les coordonnées des vecteurs \(\vec{AB}\) et \(\vec{AC}\) puis le produit scalaire \(\vec{AB}.\vec{AC}\)
Solution
\(\vec{AB}=\begin{pmatrix}-6-(-2)\\2-(-1)\end{pmatrix}=\begin{pmatrix}-4\\3\end{pmatrix}\)
\(\vec{AC}=\begin{pmatrix}0-(-2)\\4-(-1)\end{pmatrix}\)\(=\begin{pmatrix}2\\5\end{pmatrix}\)
\(\vec{AB}.\vec{AC}\)=\(-4 \times 2 +3 \times 5=-8+15=7\)
3. On appelle (d) la droite perpendiculaire à la droite (AB) passant par le point C.
Question
a. Donner un vecteur orthogonal à la droite (d).
Solution
\(\vec{AB}\) est un vecteur orthogonal à la droite (d).
Question
b. En déduire l'équation cartésienne de la droite (d).
Solution
Soit \(M(x,y)\) un point de (d) \(\vec{MC}\) est orthogonal à \(\vec{AB}\)
donc
\(\vec{MC}.\vec{AB}=\begin{pmatrix}0-x\\4-y\end{pmatrix}.\begin{pmatrix}-4\\3\end{pmatrix}=\)\(\begin{pmatrix}-x\\4-y\end{pmatrix}.\begin{pmatrix}-4\\3\end{pmatrix}\)
\(\vec{MC}.\vec{AB}=4x++3\times(4-y)=4x+12-3y\)
or \(\vec{MC}\) et \(\vec{AB}\) sont orthogonaux donc \(4x-3y+12=0\)
Question
4. Montrer que la longueur du segment [AB] est 5.
Solution
\(AB=\|\vec{AB}\|=\sqrt{(-4)^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\)
Question
5. Déduire des questions 2. et 3. la longueur du segment [AH] , H désignant le point d'intersection des droites (d) et ( AB ) .
Solution
\(\vec{AB}.\vec{AC}=\)\(\vec{AB}.\vec{AH}\) car \(\vec{AC}\) se projette orthogonalement sur \(\vec{AB}\) en \(\vec{AH}\)
donc \(\vec{AB}.\vec{AH}=7\)
AB.AH=7
5.AH=7
d'où \(AH=\frac{7}{5}\)