Exercice : Exercice 1 :
Dans chaque cas, calculer le produit scalaire \(\vec{AB}.\vec{AC}\)
Question
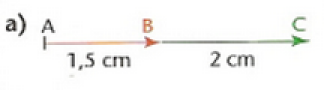
Solution
\(\vec{AB}.\vec{AC}=1,5 \times 3,5 \cos(\vec{AB},\vec{AC})=1,5 \times 3,5 \times cos(0)=5,25 \times 1 =5,25\)
Question
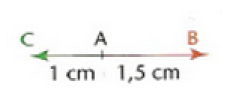
Solution
\(\vec{AB}.\vec{AC}=1 \times 1,5 \cos(\vec{AB},\vec{AC})=1 \times 1,5 \times cos(\pi)=1,5 \times (-1) =-1 ,5\)
Question
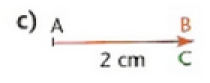
Solution
\(\vec{AB}.\vec{AB}=2 \times 2 \cos(\vec{AB},\vec{AC})=2 \times 2 \times cos(0)=4 \times 1 =4 = ||\vec{AB}||^2\)
Question
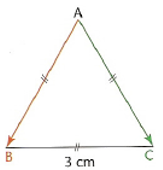
Solution
\(\vec{AB}.\vec{AB}=3 \times 3 \cos(\vec{AB},\vec{AC})=3 \times 3 \times cos(\frac{\pi}{3})=9 \times \frac{\sqrt{3}}{2} =4,5\sqrt{3}\)
Question
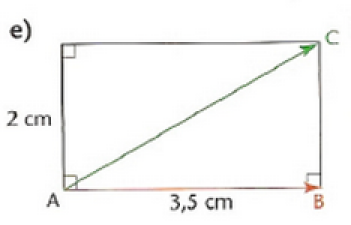
Solution
\(\vec{AB}.\vec{AC}=||\vec{AB}||\times ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=3,5 \times 3,5= 12,25 car ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=||\vec{AC}||\)
Question
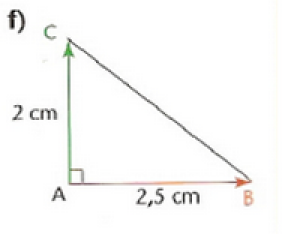
Solution
\(\vec{AB}.\vec{AC}=||\vec{AB}||\times ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=3,5 \times 2 \times cos(\frac{\pi}{2})= 0\) car les vecteurs \(\vec{AB}\) et \(\vec{AC}\) sont orthogonaux