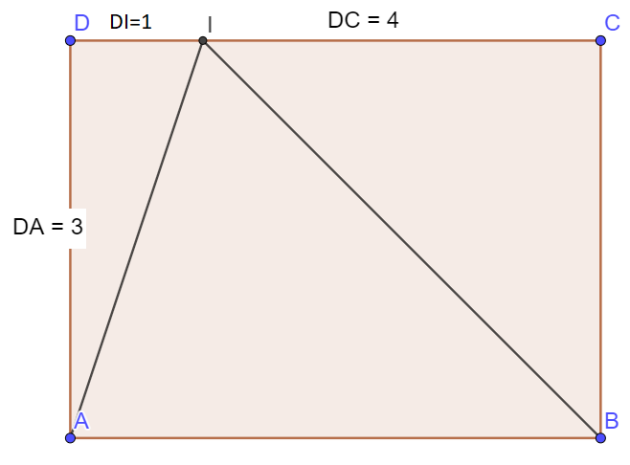
Exercice : Exercice 8 :
Question
1.Démontrer que \((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+DA^2\)
Solution
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+\vec{ID}.\vec{CB}+\vec{DA}.\vec{IC}+\vec{DA}.\vec{CB}\)
\(\vec{ID}.\vec{CB}=0\) car les vecteurs \(\vec{ID}\) et \(\vec{CB}\) sont orthogonaux
\(\vec{DA}.\vec{IC}=0\) car les vecteurs \(\vec{DA}\) et \(\vec{IC}\) sont orthogonaux
donc
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+\vec{DA}.\vec{CB}\)
or \(\vec{DA}=\vec{CB}\)
d'où
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+\vec{DA}.\vec{DA}\)
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+\vec{DA}^2\)
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{ID}.\vec{IC}+DA^2\)
Question
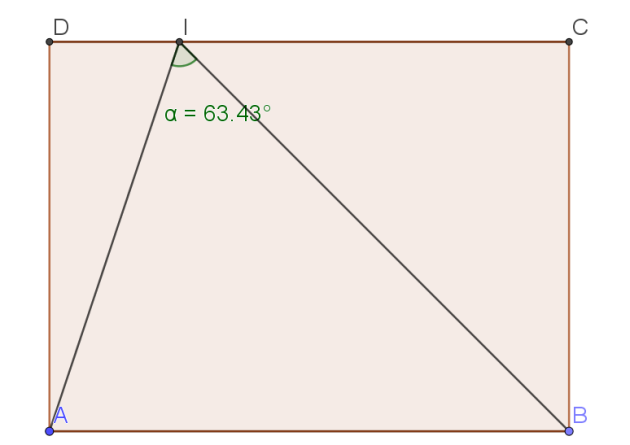
2.En déduire que \(cos(\widehat{AIB})=\frac{1}{\sqrt{5}}\) et en déduire la mesure de l'angle \(\widehat{AIB}\) en degré à \(10^{-2}\) près.
Solution
\((\vec{ID}+\vec{DA}).(\vec{IC}+\vec{CB})=\vec{IA}.\vec{IB}\) par le théorème de Chasles
donc \(\vec{IA}.\vec{IB}=\vec{ID}.\vec{IC}+DA^2\)
or \(\vec{IA}.\vec{IB}=IA \times IB \times cos((\vec{IA},\vec{IB})=IA \times IB \times cos(\widehat{AIB})\)
Dans le triangle AID rectangle en D , d'après le théorème de Pythagore:
\(AI^2=AD^2+DI^2\)
\(AI^2=3^2+1^2=9+1=10\)
\(AI=\sqrt{10}\)
Dans le triangle ICB rectangle en C , d'après le théorème de Pythagore:
\(IB^2=IC^2+CB^2\)
\(IB^2=(4-1)^2+3^2=9+9=18\)
\(IB=\sqrt{18}\)
\(\vec{IA}.\vec{IB}=IA \times IB \times cos(\widehat{AIB})\)
\(\vec{IA}.\vec{IB}=\sqrt{10} \times \sqrt{18} \times cos(\widehat{AIB})\)
d'après ce qu'on a déjà écrit :\(\vec{IA}.\vec{IB}=\vec{ID}.\vec{IC}+DA^2\)
Calculons \(\vec{ID}.\vec{IC}+DA^2=ID \times IC \times cos(\pi)+3^2=1 \times 3 \times (-1)+9=-3+9=6\)
donc \(\sqrt{10} \times \sqrt{18} \times cos(\widehat{AIB})=6\)
\(cos(\widehat{AIB})=\frac{6}{\sqrt{10} \times \sqrt{18}}\)
\(cos(\widehat{AIB})=\frac{\sqrt{36}}{\sqrt{10} \times \sqrt{18}}\)
\(cos(\widehat{AIB})=\frac{\sqrt{36}}{\sqrt{180}}\)
\(cos(\widehat{AIB})=\frac{1}{\sqrt{5}}\)
\(\widehat{AIB}=Arccos(\frac{1}{\sqrt{5}})\)
On en déduit que \(\widehat{AIB}\simeq63,43°\)