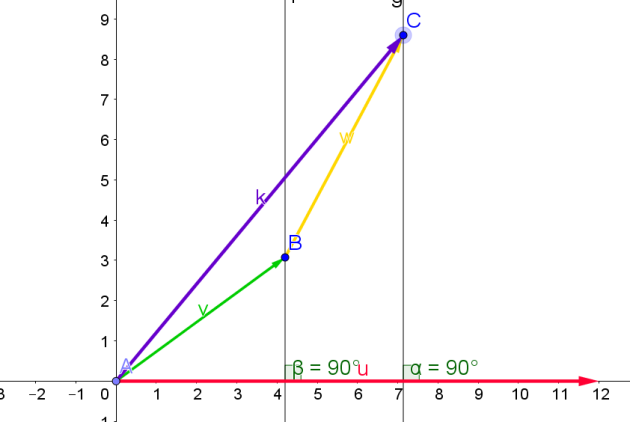
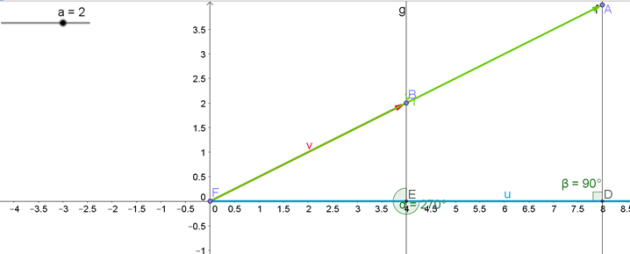
3) Propriété du produit scalaire
Fondamental : Propriété
\(\color{red}{\textbf{Pour tout vecteur } \vec{u} \textbf{ et } \vec{v} \textbf{ , on a} :}\)
\(\color{red}{\vec{u}.\vec{v} =\vec{v}.\vec{u}}\)
Complément : Démonstration
Si \(\vec{u}\) ou \(\vec{v}\)est égal au vecteur nul alors \(\vec{u}.\vec{v} =0\) et \(\vec{v}.\vec{u}=0\)
donc \(\vec{u}.\vec{v}=\vec{v}.\vec{u}\)
On suppose que\(\vec{u}\) et \(\vec{v}\) sont des vecteurs différents du vecteur nuls (démonstration évidente dans la cas contraire).
\(\vec{u}.\vec{v}\)=\(\|\vec{u}\|.\|\vec{v}\|\).cos(\(\vec{u} ;\vec{v}\) )
=\(\|\vec{v}\|.\|\vec{u}\|\).cos(\(\vec{u} ;\vec{v}\) )
=\(\|\vec{v}\|.\|\vec{u}\|\).cos(-(\(\vec{v} ;\vec{u}\)))
=\(\|\vec{v}\|.\|\vec{u}\|\).cos(\(\vec{v} ;\vec{u}\))
=\(\vec{v}.\vec{u}\)
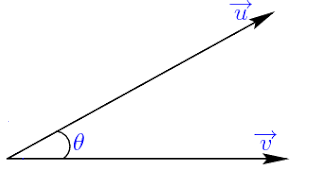
Fondamental : Propriétés
Pour tous vecteurs \(\vec{u}\), \(\vec{v}\) et \(\vec{w}\), on a :
1.\(\color{red}{\vec{u}.(\vec{v}+\vec{w} )=\vec{u}.\vec{v}+\vec{u}.\vec{w}}\)
2. \(\color{red}{\vec{u}.(k\vec{v} )=k\vec{u}.\vec{v}}\), avec k un nombre réel.