Exercice : Exercice 2 :

Calculer le produit scalaire \(\vec{AB}.\vec{AC}\) dans chacun des cas suivants :

Exercice 1.ggb [ggb, 17,3 ko]

Question

1.\(AB=3 AC=5\) et \(\widehat{BAC}=\frac{\pi}{6}\)

Solution

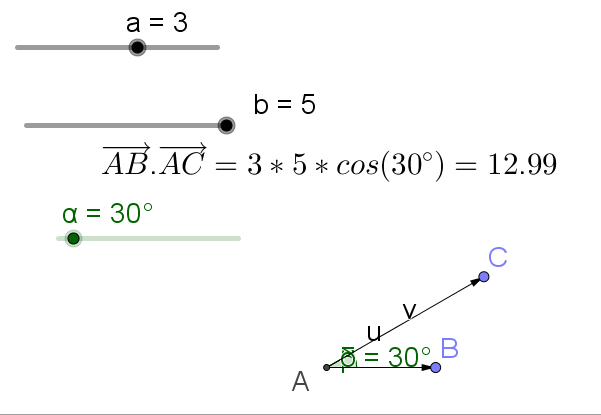
\(\vec{AB}.\vec{AC}=||\vec{AB}||\times ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=3 \times 5 \times cos(\frac{\pi}{6})=15 \times \frac{\sqrt{3}}{2}=7,5\sqrt{3}\simeq12,99\)

Question

2.AB=1 AC=2 et \((\vec{AB},\vec{AC})\)=\(\frac{2\pi}{3}\)

Solution

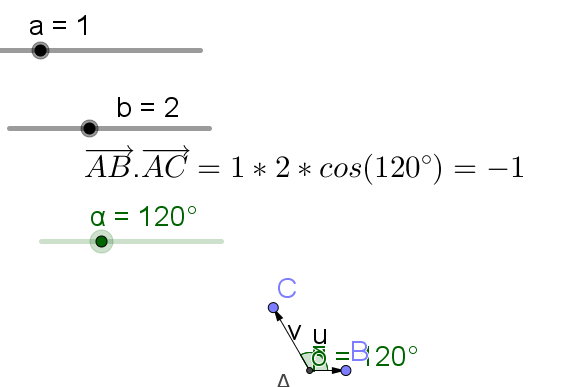
\(\vec{AB}.\vec{AC}=||\vec{AB}||\times ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=1 \times 2 \times cos(\frac{2\pi}{3})= 2 \times \frac{-1}{2}=-1\)

Question

3.BA=2 CA=2 et \(\widehat{CAB}=\frac{3\pi}{4}\)

Solution

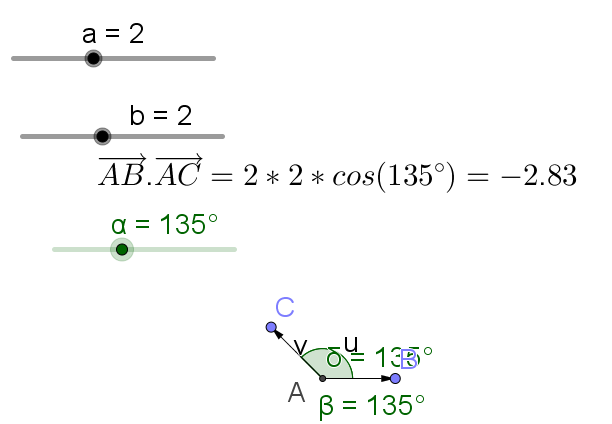
\(\vec{AB}.\vec{AC}=||\vec{AB}||\times ||\vec{AC}|| \times cos((\vec{AB},\vec{AC})=2 \times 2 \times cos(\frac{3\pi}{4})= 4 \times \frac{-\sqrt{2}}{2}=-2\sqrt{2}\) (valeur approchée -2,83)