III. Définition et propriétés du produit scalaire
Définition :
\(\color{red}{\textbf{Soit } } \vec{u} \textbf{ et } \vec{v} \textbf{ deux vecteurs du plan. }\)
\(\color{red}{\textbf{On appelle produit scalaire de } \vec{u} \textbf{ par } \vec{v} \textbf{ , noté } \vec{u}.\vec{v} \textbf{ , le nombre réel définit par : }}\)
\(- \color{red} {\vec{u}.\vec{v} =0} \textbf{ , si l'un des deux vecteurs} \vec{u} \textbf{ ou } \vec{v} \textbf{ est égal au vecteur nul}\)
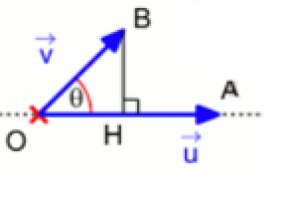
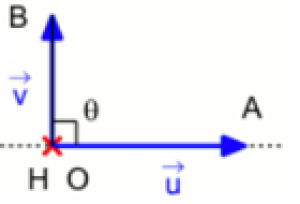
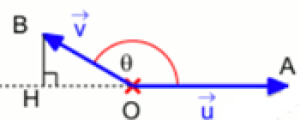
\(- \color{red} {\vec{u}.\vec{v}=\|\vec{u}\|\|\vec{v}\|cos(\vec{u};\vec{v}) \textbf{ , dans le cas contraire.} }\)
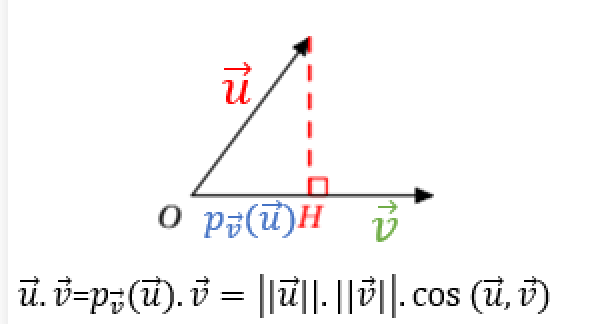
Attention :
\(\color{red}{\text{Le produit scalaire de deux vecteurs est un nombre réel. }}\)
Ecrire par exemple \(\vec{u}.\vec{v}\)=\(\vec{0}\) est une maladresse à éviter !
Remarque :
Le produit scalaire ne dépend pas des représentants choisis.
Soit un vecteur \(\vec{u}\), on a :
\(\vec{u}.\vec{u}=\|\vec{u}\|\|\vec{u}\|cos(\vec{u};\vec{u})\)
\(=\|\vec{u}\|\|\vec{u}\|cos(0)=\|\vec{u}\|^2\)
Fondamental :
\(\color{magenta}{\text{1er cas :}}\)
L'angle des deux vecteurs est aigu.
Le produit scalaire est positif.
\(\vec{u}.\vec{v}\) = OA.OH où
H est le projeté orthogonal de B sur (OA)
\(\color{magenta}{\text{2ème cas :}}\)
L'angle des deux vecteurs est droit.
Le produit scalaire est nul.
\(\vec{u}.\vec{v}\) = 0
\(\color{magenta}{\text{3ème cas :}}\)
L'angle des deux vecteurs est obtus.
Le produit scalaire est négatif.
\(\vec{u}.\vec{v}\) = - OA.OH
où H est le projeté orthogonal de B sur (OA)
Rappel : Norme d'un vecteur
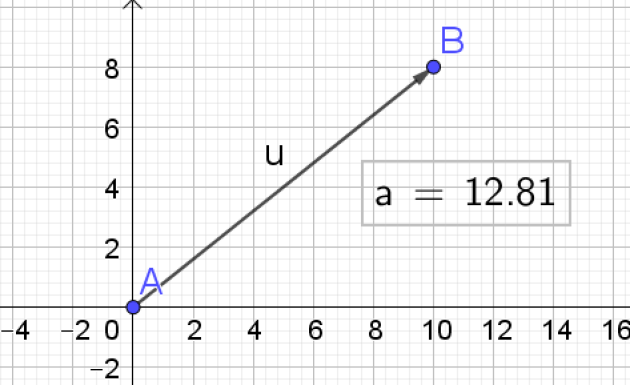
Soit un vecteur \(\vec{u}\) et deux points A et B tels que \(\vec{u}=\vec{AB}\)
La norme du vecteur \(\vec{u},\) notée\( \|\vec{u}\|\), est la distance AB.
\(||\vec{u}||=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(||\vec{u}||=\sqrt{(10-0)^2+(8-0)^2}\)
\(||\vec{u}||=\sqrt{100+64}\)
\(||\vec{u}||=\sqrt{164}\simeq12,81\)