Exercice : Exercice 34 :
Le plan est rapporté à un repère orthonormé \((O;\vec{\imath},\vec{\jmath}\)
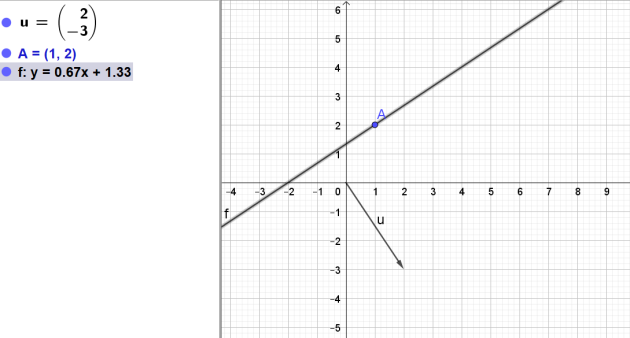
On considère le vecteur \(\vec{u}\) de coordonnées \(\left( \begin{array}{c}2 \\-3\end{array} \right)\) et le point A de coordonnées (1 ;2)
Question
1.Faire un dessin.Représenter l'ensemble des points M du plan tels que \(\vec{AM}\) est orthogonal à \(\vec{u}\)
Question
2. Démontrer que l'ensemble des ces points est une droite dont on donnera une équation.
Solution
\(\vec{AM}=\left( \begin{array}{c}x-1 \\y-2\end{array} \right)\)
\(\vec{AM}\) est orthogonal à \(\vec{u}\) \(\Longleftrightarrow\) \(\vec{AM}\).\(\vec{u}=0\)
\(\Longleftrightarrow\) \(\left( \begin{array}{c}x-1 \\y-2\end{array} \right).\left( \begin{array}{c}2 \\-3\end{array} \right)=0\)
\(\Longleftrightarrow\) \((x-1) \times 2 +(y-2) \times (-3)=0\)
\(\Longleftrightarrow\) \(2x-2 -3y+6=0\)
\(\Longleftrightarrow\) \(2x -3y+4=0\)
\(\Longleftrightarrow\) \(y=\frac{2}{3}x+\frac{4}{3}\)