Exercice : Exercice 17 :
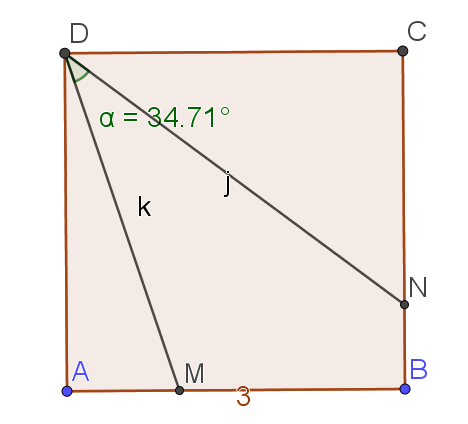
Soit ABCD un carré de côté 3 cm.
Soit M un point de [AB] tel que \(\vec{AM}=\frac{1}{3}\vec{AB}\) et N un point de [BC] tel que
\(\vec{BN}=\frac{1}{4}\vec{BC}\)
Question
1.Faire une figure
Question
2. Déterminer les coordonnées des points D,M et N dans le repère \((A,\vec{AB},\vec{AD})\) en déduire le produit scalaire \(\vec{DM}.\vec{DN}\)
Solution
\(D(0,1) ,M(\frac{1}{3},0) et N(1,\frac{1}{4})\) dans le repère \((A,\vec{AB},\vec{AD})\)
\(\vec{DM}=\begin{pmatrix}\frac{1}{3}-0\\0-1\end{pmatrix}=\begin{pmatrix}\frac{1}{3}\\-1\end{pmatrix}\)
\(\vec{DN}=\begin{pmatrix}1-0\\\frac{1}{4}-1\end{pmatrix}=\begin{pmatrix}1\\\frac{-3}{4}\end{pmatrix}\)
\(\iff \vec{DM}.\vec{DN}=\begin{pmatrix}\frac{1}{3}\\-1\end{pmatrix}.\begin{pmatrix}1\\\frac{-3}{4}\end{pmatrix}\)
\(\iff \vec{DM}.\vec{DN}=(\frac{1}{3}.1)+(-1)\times(\frac{-3}{4})\)
\(\iff \vec{DM}.\vec{DN}=\frac{1}{3}+\frac{3}{4}\)
\(\iff \vec{DM}.\vec{DN}=\frac{4}{12}+\frac{9}{12}\)
\(\iff \vec{DM}.\vec{DN}=\frac{13}{12}\)
Question
3.En utilisant le théorème de Pythagore dans des triangles rectangles à spécifier, déterminer les longueurs DM et DN
Solution
DM=\(\|\vec{DM}\|=\sqrt{(\frac{1}{3})^2+(-1)^2}=\sqrt{\frac{1}{9}+1}=\sqrt{\frac{1}{9}+\frac{9}{9}}=\frac{\sqrt{10}}{3}\)
DN=\(\|\vec{DN}\|=\sqrt{1^2+(\frac{-3}{4})^2}=\sqrt{1+\frac{9}{16}}=\sqrt{\frac{16}{16}+\frac{9}{16}}=\sqrt{\frac{25}{16}}=\frac{5}{4}\)
Question
4.En écrivant que \(\vec{DM}.\vec{DN}=DM×DN×cos((\vec{DM},\vec{DN}) ̂)\) et en utilisant la question précédente
déterminer la valeur de \(cos((\vec{DM},\vec{DN}) ̂)\) puis la mesure de l'angle de vecteurs \((\vec{DM},\vec{DN}) ̂\)
Solution
\(\vec{DM}.\vec{DN}=\|\vec{DM}\|.\|\vec{DN}\| .cos(\vec{DM},\vec{DN})\)=\(\frac{13}{12}\)
\(\iff \frac{\sqrt{10}}{3}. \frac{5}{4} .cos(\vec{DM},\vec{DN})\)=\(\frac{13}{12}\)
\(cos(\vec{DM},\vec{DN})=\frac{\frac{13}{12}}{\frac{\sqrt{10}}{3}. \frac{5}{4}}\)
\(\iff cos(\vec{DM},\vec{DN})=\frac{\frac{13}{12}}{\frac{5\sqrt{10}}{12}}\)
\(\iff cos(\vec{DM},\vec{DN})\)=\(\frac{13}{12} \times \frac{12}{5\sqrt{10}}\)
\(\iff cos(\vec{DM},\vec{DN})\)=\(\frac{13}{5\sqrt{10}}\)
\(\iff (\vec{DM},\vec{DN})=Arccos(\frac{13}{5\sqrt{10}})\simeq34,9°\)