Exercice : Exercice 42 :
Question
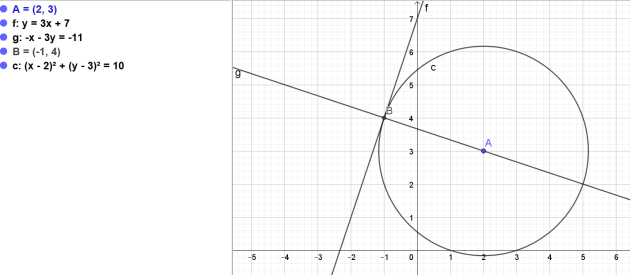
1.Déterminer le rayon du cercle de centre A tangent à la droite D
Solution
Un vecteur directeur de la droite D est \(\vec{u}=(1 ;3)\)
1.Déterminons les coordonnées du point \( B(x,y)\) : point de tangence de la droite D au cercle de centre A.
\(\vec{AB}.\vec{u}=0\)
\(\left( \begin{array}{c}x-2 \\y-3\end{array} \right).\left( \begin{array}{c}1 \\3\end{array} \right)=0\)
\((x-2) \times 1+ (y-3) \times 3=0\)
\(x-2+3y-9=0\)
\(x+3y-11=0\)
\(3y=-x+11\)
\(\color{red}{y=-\frac{1}{3}x+\frac{11}{3}}\)
\(\begin{cases}{y=-\frac{1}{3}x+\frac{11}{3}\\y =3x+7}\end{cases}\)
\(-\frac{1}{3}x+\frac{11}{3} =3x+7\)
\(-\frac{1}{3}x-3x =7-\frac{11}{3}\)
\(-\frac{1}{3}x-\frac{3}{1}x =\frac{7}{1}-\frac{11}{3}\)
\(-\frac{1}{3}x-\frac{9}{3}x =\frac{21}{3}-\frac{11}{3}\)
\(-\frac{10}{3}x =\frac{10}{3}\)
donc \(x=-1\) et \(y=3\times (-1) +7=4\)
Calcul du rayon du cercle :
R=AB=\(\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-1-2)^2+(4-3)^2}=\sqrt{(-3)^2+(1)^2}=\sqrt{9+1}=\sqrt{10}\)
Le rayon du cercle est donc \(\sqrt{10}\)
Question
2.Déterminer une équation du cercle de centre A tangent à la droite D
Solution
\(AM^2=R^2\)
donc \((\sqrt{(x- 2)^2 + (y- 3)^2})^2=\sqrt{10}^2\)
\(\iff (x- 2)^2 + (y- 3)^2=10\)