Exercice : Exercice 24 :
Calculer \(cos(2x)\) dans les deux cas suivants :
Question
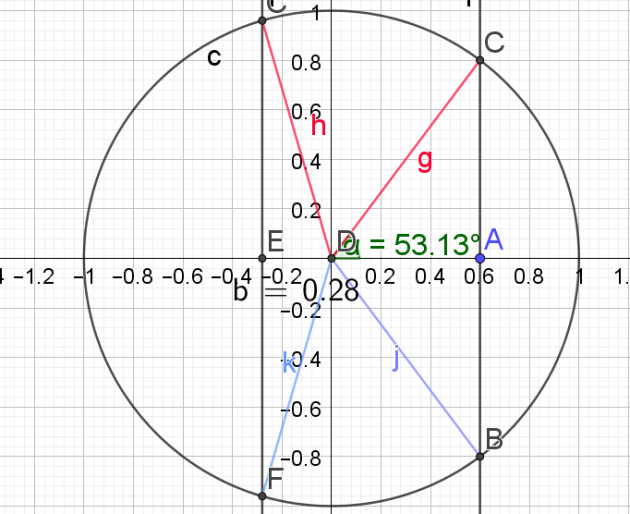
a. \(cos x=\frac{3}{5}\)\(\)
Solution
Comme on nous donne les valeurs du cosinus de l'angle, il faudra utiliser la formule :
\(cos(2a)=2cos^2(a)-1\) (le sinus de l'angle n'étant pas connu)
\(cos(2a)=2(\frac{3}{5})^2-1\)
\(cos(2a)=2(\frac{9}{25})-1\)
\(cos(2a)=(\frac{18}{25})-1\)
\(cos(2a)=(\frac{18}{25})-(\frac{25}{25})\)
\(\color{magenta}{cos(2a)=-\frac{7}{25}=-0,28}\)
\(\begin{cases}Arccos(\frac{3}{5} )\simeq53,13°\\Arccos(-\frac{7}{25} )\simeq106,26°\end{cases}\)
Question
\(b. sin x=-\frac{1}{3}\)\(\)
Solution
Comme on nous donne les valeurs du sinus de l'angle, il faudra utiliser la formule :
\(cos(2a)=1-2sin^2(a)\) (le cosinus de l'angle n'étant pas connu)
\(cos(2a)=1-2(-\frac{1}{3})^2\)
\(cos(2a)=1-2(\frac{1}{9})\)
\(cos(2a)=1-\frac{2}{9}\)
\(cos(2a)=(\frac{9}{9})-(\frac{2}{9})\)
\(\color{magenta}{cos(2a)=\frac{7}{9}\simeq0,78}\)
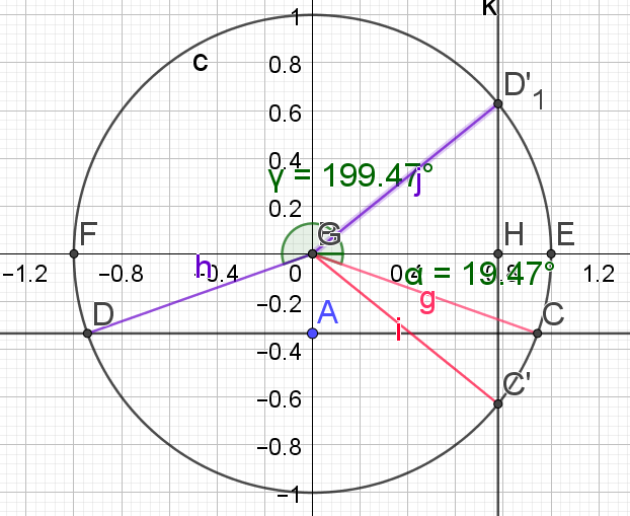
\(\begin{cases}Arcsin(\frac{-1}{3} )\simeq-19,47°\\Arccos(\frac{7}{9} )\simeq38,94°\end{cases}\)
\(a=(\vec{GE},\vec{GD})=(\vec{GE},\vec{GF})-(\vec{GF},\vec{GD})\simeq-180+19 ,47\simeq-160,53\)
\(2a\simeq 2 \times (-160,53)=-321,06\) qui correspond au même point sur le cercle trigonométrique que 360-321,06=38,94°
Question
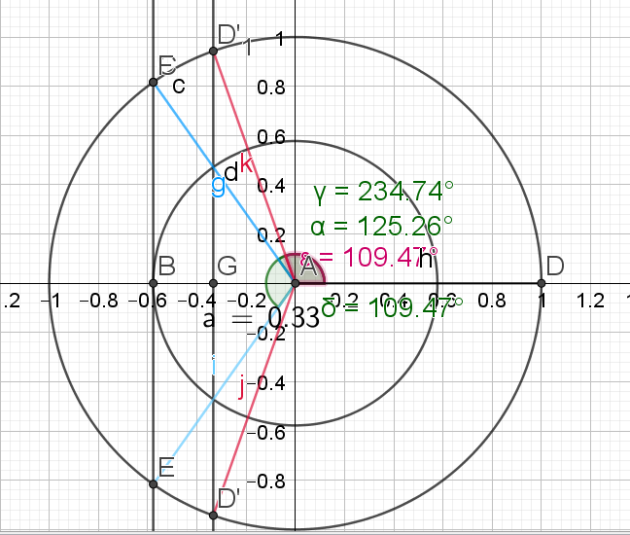
c.\(cos x = -\frac{\sqrt{3}}{3}\)
Solution
\(cos a = -\frac{\sqrt{3}}{3}\)
Comme on nous donne les valeurs du cosinus de l'angle, il faudra utiliser la formule :
\(cos(2a)=2cos^2(a)-1\) (le sinus de l'angle n'étant pas connu)
\(cos(2a)=2(-\frac{\sqrt{3}}{3})^2-1\)
\(cos(2a)=2(\frac{3}{9})-1\)
\(cos(2a)=(\frac{2}{3})-1\)
\(cos(2a)=\frac{-1}{3}\)
\(\color{magenta}{cos(2a)=-\frac{1}{3}}\)
\(\begin{cases}Arccos(-\frac{\sqrt{3}}{3})\simeq125,26°\\Arccos(-\frac{1}{3} )\simeq109,47°\end{cases}\)