VIII. Equations de cercles
Complément :
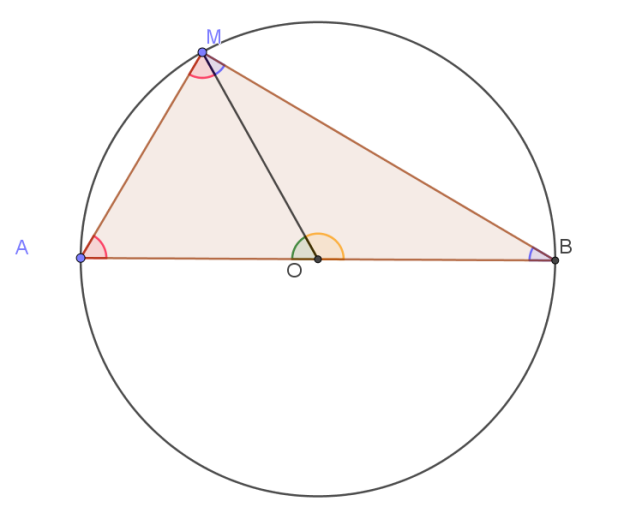
Fondamental : Théorème
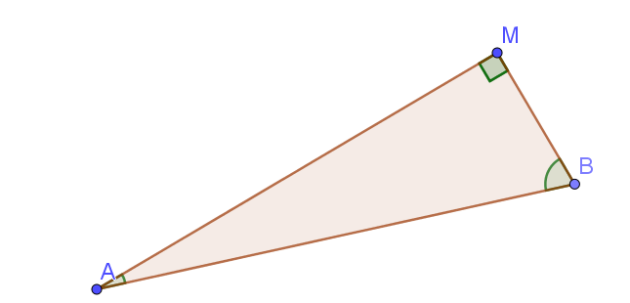
\(\color{red}{\textbf{Si un triangle est rectangle alors il est inscrit dans un demi-cercle dont un des diamètres est son hypoténuse.}}\)
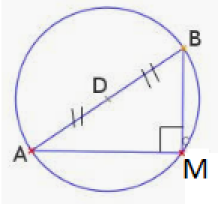
Complément : Démonstration
Soit ABM un triangle rectangle en M
1. Construire le point N symétrique de M par rapport au milieu O de [AB]
2. Montrer que AMBN est un rectangle.
3. Conclure.
Complément :
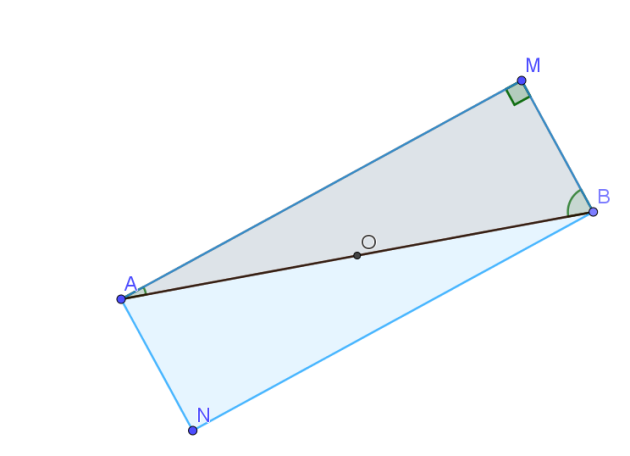
Le quadrilatère AMBN a ses diagonales qui ont même milieu.
En effet :
O est le milieu de [AB] car O est le milieu du segment [AB].
O est le milieu de [MN] car N est le symétrique de M par rapport à O
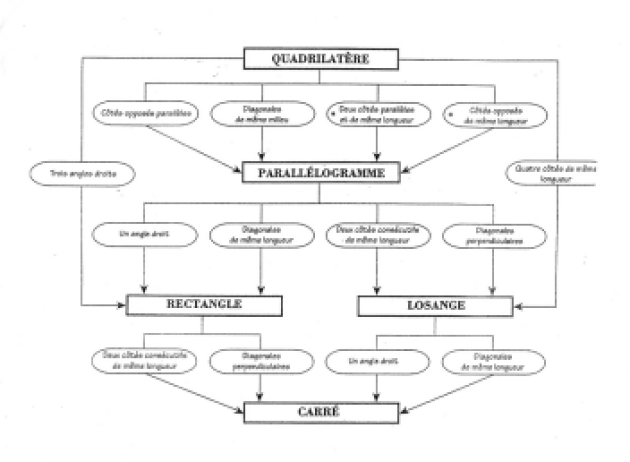
donc le quadrilatère AMBN est un \(\color{magenta}{parallélogramme}\)
De plus le parallélogramme AMBN a un angle droit \(\widehat{AMB}\).
Donc le parallélogramme AMBN est un \(\color{magenta}{rectangle}\).
Or un rectangle a ses diagonales qui se coupent en leurs milieux et qui ont même longueur.
\(\color{red}{\textbf{On en déduit que OA=OB=OM=ON }}\)
\(\color{red}{\textbf{donc les points M et N sont situés sur le cercle de centre 0 et de diamètre [AB] }}\)
\(\color{red}{\textbf{donc le théorème est démontré.}}\)
Fondamental : Théorème Réciproque
\(\color{red}{\textbf{Si un triangle est inscrit dans un cercle dont un côté est un diamètre }}\)
\(\color{red}{\textbf{alors le triangle est un triangle rectangle et ce diamètre est son hypoténuse.}}\)
Complément : Démonstration
On sait que :
- O est le centre du cercle
- [AB] est un diamètre du cercle
- M est un point du cercle.
On veut prouver que le triangle ABM est rectangle en M.
\(\color{magenta}{\textbf{A. Première démonstration :}}\)
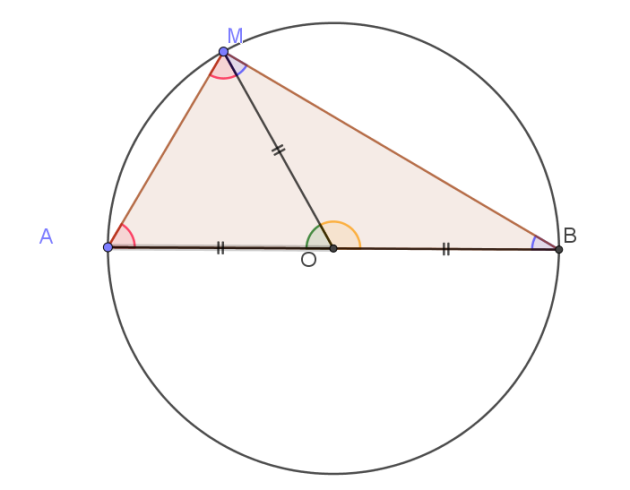
1. Que peut on dire des triangles OAM et OBM ?
2. On pose \(\widehat{OMA}= x\). Calculer \(\widehat{MOA}\) en fonction de \(x\).
3. Calculer \(\widehat{MOB}\) , puis \(\widehat{OMB}\), en fonction de \(x\) .
4. En déduire \(\widehat{AMB}\) . Conclure.
Complément :
1. Les triangles OAM et OBM sont isocèles en O car OA=OB=OM=R : les segments [OA],[OB] et [OM] sont des rayons du cercle
2. OAM est un triangle isocèle en O donc \(\widehat{OMA}=\widehat{OAM}= x\)
La somme des trois mesures des angles d'un triangle vaut 180°.
\(\widehat{OMA}+\widehat{OAM}+\widehat{MOA}=\pi\)
\(\Longleftrightarrow\) \(x+x+\widehat{MOA}=\pi\)
d'où \(\color{red}\widehat{MOA}=\pi-2x\)
3. \(\widehat{MOB} +\widehat{MOA}=\pi\) (La mesure d'un angle plat est de 180°)
\(\widehat{MOB}+\pi-2x=\pi\)
\(\Longleftrightarrow\) \(\widehat{MOB}=\pi-(\pi-2x)=\pi-\pi+2x=2x\)
\(\color{red}\Longleftrightarrow\widehat{MOB}=2x\)
La somme des trois mesures des angles d'un triangle vaut 180° donc :
\(\widehat{OMB}\)+ \(\widehat{OBM}\)+\(\widehat{MOB}=\pi\)
\(\Longleftrightarrow\)\(\widehat{OMB}+ \widehat{OBM}+2x=\pi\)
or \(\widehat{OMB}= \widehat{OBM}\) car le triangle OBM est isocèle en O
\(\Longleftrightarrow\)\(2\widehat{OMB}+2x=\pi\)
\(\Longleftrightarrow\)\(2\widehat{OMB}=\pi-2x\)
\(\color{red}\Longleftrightarrow\widehat{OMB}=\frac{\pi}{2}-x\)
4. \(\widehat{AMB}=\widehat{AMO}+\widehat{OMB}=x+\frac{\pi}{2}-x=\frac{\pi}{2}\)
donc \(\color{red}\widehat{AMB}=\frac{\pi}{2}\)
\(\color{red}{\textbf{On en déduit que le triangle AMB est rectangle en A }}\)
\(\color{red}{\textbf{et donc le théorème est démontré.}}\)
Complément :
\(\color{magenta}{\textbf{B. Deuxième démonstration :}}\)
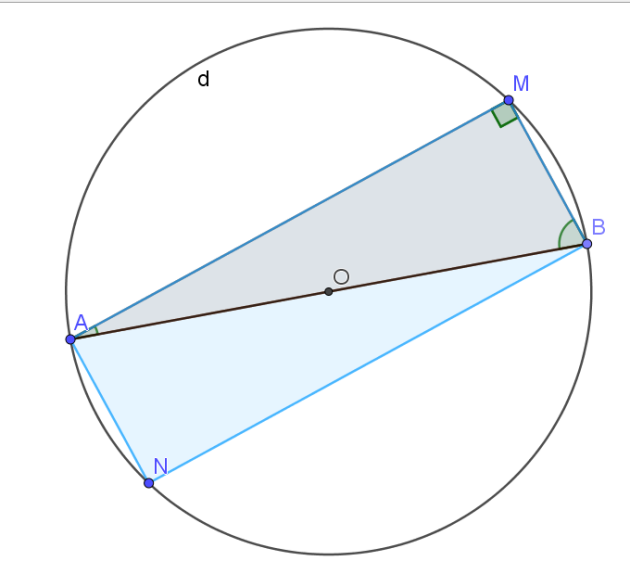
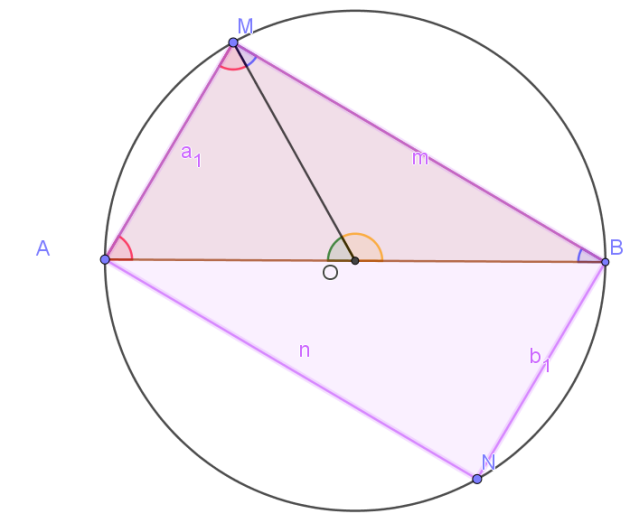
1. Construire le point N, symétrique de M par rapport à O.
2. Quelle est la nature de AMBN ?
3. Que peut on en déduire ?
Complément :
Le quadrilatère AMBN a ses diagonales qui ont même milieu.
En effet :
O est le milieu de [AB] car O est le centre du cercle et [AB] est un diamètre.
O est le milieu de [MN] car N est le symétrique de M par rapport à O
donc le quadrilatère AMBN est un \(\color{magenta}{parallélogramme}\)
De plus le parallélogramme AMBN a ses diagonales de même longueur car :
OA=OB=R ce sont les deux extrémités d'un même diamètre.
OM=ON=R car M est un point du cercle donc OM=R et ON=OM car N est le symétrique de M par rapport à O.
Donc le parallélogramme AMBN est un \(\color{magenta}{rectangle}\).
\(\color{red}{\textbf{On en déduit que l'angle } \widehat{AMB} \textbf{est rectangle en A et donc le théorème est démontré.}}\)
Fondamental : Théorème ( Conséquence)
\(\color{red}{\textbf{Si dans un triangle, }}\)
\(\color{red}{\textbf{le milieu d'un côté est à égale distance des trois sommets du triangle , }}\)
\(\color{red}{\textbf{alors ce triangle est rectangle.}}\)
Complément : Démonstration
OA = OB = OM donc le cercle de centre O qui a pour diamètre [AB] passe par M.
Donc le triangle ABC est rectangle en C, d'après la propriété précédente.
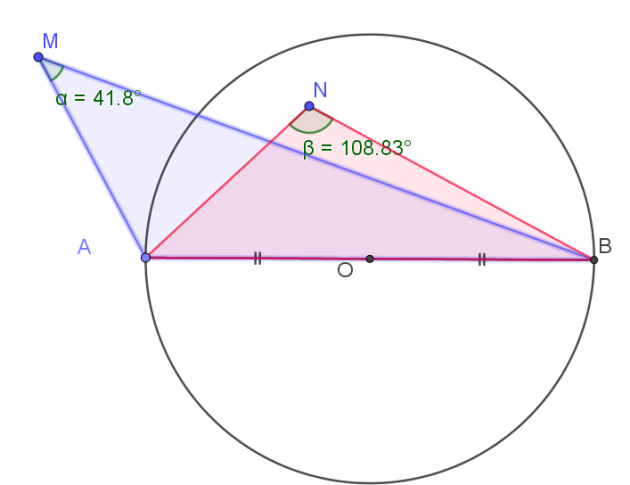
Remarque :
\(\color{magenta}{\textbf{Si le point M est à l'extérieur du cercle de diamètre [AB] l'angle }\widehat{AMB} \textbf{ est aigu.}}\)
\(\color{magenta}{\textbf{Si le point N est dans le disque de diamètre [AB] , l'angle } \widehat{AMB} \textbf{ est obtus.}}\)
Fondamental : Théorème
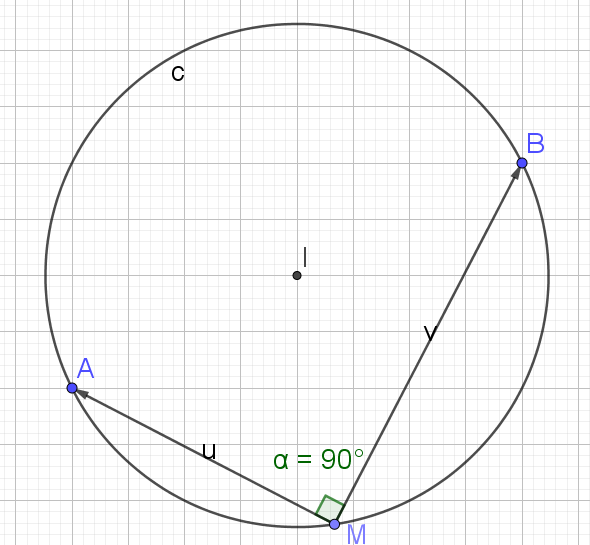
\(\color{red}{\textbf{ L'ensemble des points M tels que } \vec{MA}.\vec{MB}=0 \textbf{ est le cercle dont un des diamètres est [AB]}}\)
Exemple :
\(\color{magenta}{\text{Exercice 36 à 38}}\)
Complément : Démonstration :
\(\vec{MA}.\vec{MB}=0\)
\(\Longleftrightarrow\) \(\vec{MA}\) et \(\vec{MB}\) sont orthogonaux.
\(\Longleftrightarrow\) \((MA)\) et\((MB)\) sont perpendiculaires.
\(\Longleftrightarrow\) MAB est un triangle rectangle en M.
\(\Longleftrightarrow\) MAB est inscrit dans un le demi-cercle dont un des diamètres est [AB]
Fondamental :
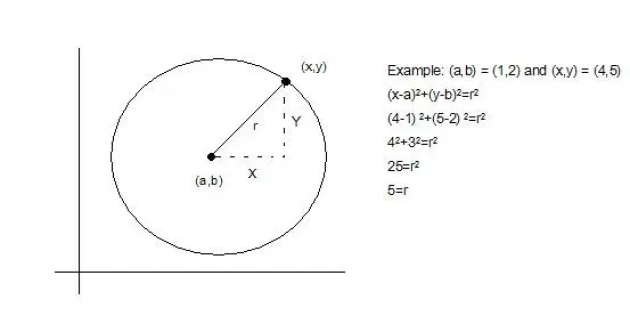
\(\color{red}{\textbf{Dans un repère orthonormé, le cercle C de centre Ω(a,b) et de rayon R a pour équation :}}\)
\(\color{red}{(x-a)^2+(y-b)^2=R^2}\)
Exemple :
\(\color{magenta}{\text{Exercice 39-42}}\)
Fondamental : Propriété
\(\color{red}{\textbf{Le plan est muni d'un repère } (O;\vec{i};\vec{j}) \textbf{orthonormal.}}\)
\(\color{red}{\textbf{Soit } A(x_A ; y_A) \textbf{ ; } B(x_B ; y_B)}\)
\(\color{red}{\textbf{et } \mathcal{C} \textbf{le cercle de diamètre [AB].}}\)
\(\color{red}{\textbf{Alors tout point M de } \mathcal{C} \textbf{ a ses coordonnées qui vérifient :}}\)
\(\color{red}{(x −x_A)(x −x_B)+(y − y_A)(y − y_B) = 0}\)
Complément :
On se place dans un repère orthonormé \((O ;\vec{i} ; \vec{j} )\).
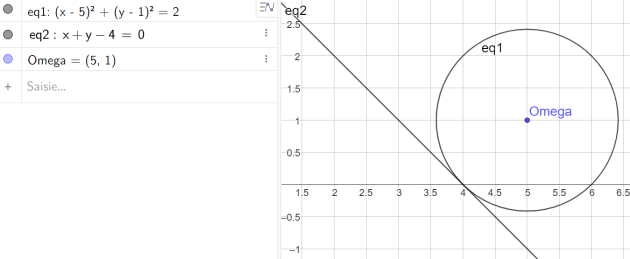
Déterminer l'équation du cercle de centre \(\Omega(5 ; 1)\)
et tangent à la droite \(\mathbb{D}\) d'équation : \(x + y – 4 = 0\)
Calcul du rayon du cercle :
d(\Omega,\(\mathbb{D}\)) = \(\frac{|5+1-4|}{\sqrt{1^2 +1^2}}=\frac{2}{\sqrt{1+1}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
L'équation du cercle est donc :
\((x-5)^2+(y-1)^2=\sqrt{2}^2\)
\(\iff (x-5)^2+(y-1)^2=2\)
