Formule d'Al-Kashi Mathématicien perse (1380-1429)
Complément :
Fondamental :
\(\color{magenta}{\textbf{Formule d'Al Kashi}}\)
\(AB^2=AC^2+BC^2-2AC × BC ×cos(\widehat{ACB})\)
\(a^2=b^2+c^2-2bc cos \widehat{A}\)
\(b^2=a^2+c^2-2ac cos \widehat{B}\)
\(c^2=a^2+b^2-2ab cos \widehat{C}\)
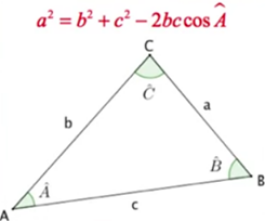
Complément : Démonstration :
\(\color{magenta}{\textbf{Démontrons que : } c^2=a^2+b^2-2ab cos \widehat{ACB}}\)
En écrivant \(\vec{AB}=\vec{AC}+\vec{CB}\) grâce à la relation de Chasles.
\(AB^2=\|\vec{AB}\|^2=\|\vec{AC}+\vec{CB}\|^2\)
donc \(AB^2=(\vec{AC}+\vec{CB}).(\vec{AC}+\vec{CB})=(\vec{AC}-\vec{BC})(\vec{AC}-\vec{BC})\)
\(AB^2=\vec{AC}^2-2\vec{AC}.\vec{BC}+\vec{BC}^2\)
\(AB^2=AC^2-2\vec{AC} . \vec{BC}+BC^2\)
\(AB^2=AC^2-2AC . BC ×cos(\widehat{ACB})+BC^2\)
donc \(c^2=a^2+b^2-2ab cos \widehat{ACB}\)
De même pour les autres formules :
\(a^2=b^2+c^2-2bc cos \widehat{BAC}\)
\(b^2=a^2+c^2-2ac cos \widehat{ABC}\)
Remarque :
Pour un angle droit, on retrouve le théorème de Pythagore.
\(\color{magenta}{\textbf{Pythagore (-570 à – 495 avant Jésus Christ)}}\) était un philosophe et mathématicien grec.
Puisqu'il n'a lui-même rien écrit, la plupart des informations à son sujet ont été rédigées longtemps après sa mort, et il est donc difficile de savoir avec certitude s'il est bien l'auteur de tout ce qui lui a été attribué.
Les timbres ont été émis le 20 août 1955, pour célébrer le 2500e anniversaire de la fondation de la première école de philosophie par Pythagore à Samos.
Pour en savoir plus: Wikipedia
Le timbre de 5 drachmes (monaie grecque) présente une pièce de monnaie de Samos sur laquelle figure Pythagore.
Le timbre de 6 drachmes montre une carte de l'île de Samos, lieu de naissance de Pythagore.
Sur le timbre de 3,50 drachmes, on peut voir une illustration du théorème de Pythagore :
le triangle rectangle, au centre, a pour dimensions 3,4 et 5 unités.
Ainsi, l'aire du grand carré est égale à la somme des aires des deux autres carrés : \(4^2 + 3^2 = 5^2.\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Complément :
Autre démonstration:
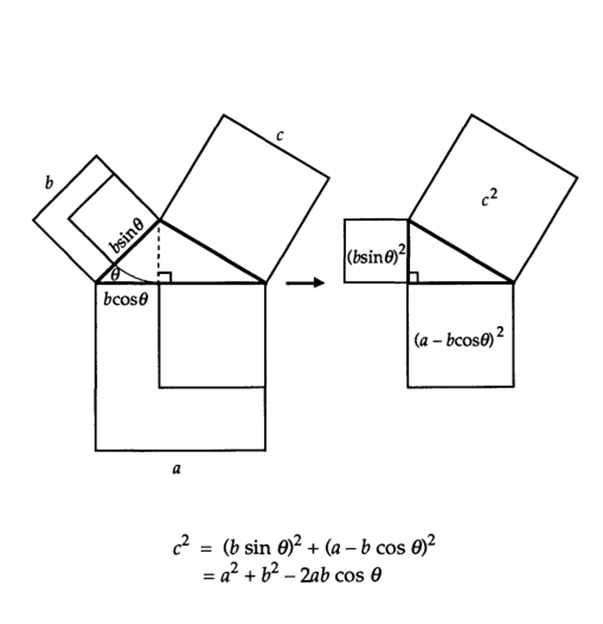
\(c^2=(bsin\theta]^2+(a-bcos\theta)^2\)
\(c^2=b^2sin^2\theta+a^2-2abcos\theta+b^2cos^2\theta\)
\(c^2=a^2+b^2(sin^2\theta+cos^2\theta)-2abcos\theta\)
or \(cos^2\theta+sin^2\theta=1\)
donc \(c^2=a^2+b^2-2abcos\theta\) Formule d'Al-Kashi
Exemple :
\(\color{magenta}{\textbf{Retour à l'exercice de début de chapitre :}}\)
ABC est un triangle tel que AB= 4 AC=3 et (\(\vec{AB},\vec{AC}\))=70°
Calculer la longueur BC arrondir au dixième.
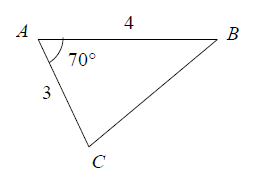
Complément :
Utilisons la formule d'Al-Kashi :
\(BC^2=AC^2+AB^2-2\vec{AC}.\vec{AB}=AC^2+AB^2-2 \times AC \times AB \times cos((\vec{AC},\vec{AB}))\)
\(BC^2=3^2+4^2-2 \times 3 \times 4 \times cos(70)=9+16-24 \times cos(70)\simeq16,79\)
\(BC\simeq\sqrt{4,1}\)