Exercice : Exercice 20 :
Soit A(-1 ;2) , B(5 ;3) et E(3 ;4) trois points du plan.
Question
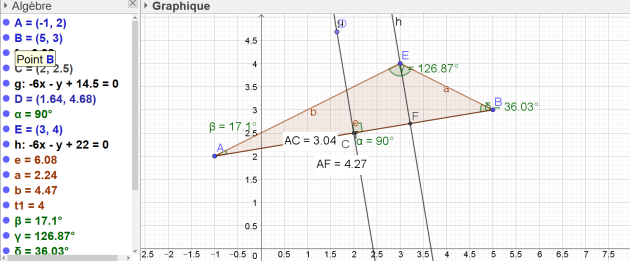
1. Faire une figure qu'on complétera au fur et à mesure de l'exercice
2.En utilisant le produit scalaire, déterminer l'équation des droites suivantes :
Question
- l'équation de la hauteur passant par le sommet E dans le triangle BAE.
Solution
Soit P un point appartenant à la hauteur du triangle ABE passant par le point E de coordonnées \((x,y)\) :
\(\vec{EP}.\vec{AB}=0\)
or \(\vec{EP}=\begin{pmatrix}x-3\\y-4\end{pmatrix}\)
\(\vec{AB}=\begin{pmatrix}5-(-1)\\3-2\end{pmatrix}\)=\(\begin{pmatrix}6\\1\end{pmatrix}\)
donc \(\vec{EP}.\vec{AB}\)=\(\begin{pmatrix}x-3\\y-4\end{pmatrix}.\begin{pmatrix}6\\1\end{pmatrix}\)=\(6(x-3)+(y-4) \times 1=0\)
donc \(6x-18+y-4=0\)
en simplifiant \(6x+y-22=0\)
L'équation de la hauteur passant par le point E dans le triangle AEB est donc \(\fbox{y=-6x+22}\)
Question
- l'équation de la droite d médiatrice du segment [AB] (la médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu)
Solution
Calcul des Les coordonnée du point C milieu de [AB] :
\(x_C=\frac{x_A+x_B}{2}=\frac{5+(-1)}{2}=2\)
\(y_C=\frac{y_A+y_B}{2}=\frac{3+2}{2}=2,5\)
Soit M un point de la médiatrice du segment [AB] ;
\(\vec{CM}=\begin{pmatrix}x-2\\y-2,5\end{pmatrix}\)
\(\vec{CM}.\vec{AB}=0\)
donc \(\begin{pmatrix}x-2\\y-2,5\end{pmatrix}.\begin{pmatrix}6\\1\end{pmatrix}=0\)
d'où \(6(x-2)+1 \times (y-2,5)=0\)
\(6x-12+y-2,5=0\)
L'équation de la médiatrice du segment [AB] est donc \(6x+y-14,5=0\) soit \(y=-6x+14,5\)
2. En utilisant le produit scalaire,
Question
a. déterminer la mesure des angles du triangle BAE.
Solution
\(\vec{AB}=\begin{pmatrix}6\\1\end{pmatrix}\)
\(AB=\sqrt{6^2+1^2}=\sqrt{36+1}=\sqrt{37}\)
\(\vec{AE}=\begin{pmatrix}3-(-1)\\4-2\end{pmatrix}\)\(=\begin{pmatrix}4\\2\end{pmatrix}\)
\(AE=\sqrt{4^2+2^2}=\sqrt{16+4}=\sqrt{20}\)
\(\vec{BE}=\begin{pmatrix}3-5\\4-3\end{pmatrix}\)\(=\begin{pmatrix}-2\\1\end{pmatrix}\)
\(BE=\sqrt{(-2)^2+1^2}=\sqrt{4+1}=\sqrt{5}\)
On utilise alors la Formule d'Al Kashi:
\(BE^2=AB^2+AE^2-2AB.AE.cos(\widehat{BAE})\)
5=37+20-2AB.AE.\(cos(\widehat{BAE})\)
\(5=57-2AB.AE.cos(\widehat{BAE})\)
-52=-2AB.AE.\(cos(\widehat{BAE})\)
-26=-2AB.AE.\(cos(\widehat{BAE})\)
26=AB.AE.\(cos(\widehat{BAE})\)
\(cos(\widehat{BAE})=\frac{26}{AB.AE}\)
\(\color{red}{cos(\widehat{BAE})=\frac{26}{\sqrt{37}.\sqrt{20}}}\)
\(\widehat{BAE}=Arccos(\frac{26}{\sqrt{37}.\sqrt{20}})\simeq \fbox{17°}\)
\(AB^2=AE^2+BE^2-2AE.BE.cos(\widehat{BEA})\)
37=20+5-2AE.BE.\(cos(\widehat{BEA})\)
\(37=25-2AE.BE.cos(\widehat{BEA})\)
12=-2AE.BE.\(cos(\widehat{BEA})\)
-6=AE.BE.\(cos(\widehat{BEA})\)
-6=AE.BE.\(cos(\widehat{BEA})\)
\(cos(\widehat{BEA})=\frac{-6}{AE.BE}\)
\(cos(\widehat{BEA})=\frac{-6}{\sqrt{20}.\sqrt{5}}=\frac{-6}{\sqrt{100}}=\frac{-6}{10}=-0,6\)
\(\widehat{BEA}=Arccos(-0,6)\simeq \fbox{127°}\)
\(AE^2=BE^2+AB^2-2BE.AB.cos(\widehat{EBA})\)
20=5+37-2BE.AB.\(cos(\widehat{EBA})\)
\(20=42-2BE.AB.cos(\widehat{EBA})\)
-22=-2BE.AB.\(cos(\widehat{EBA})\)
11=BE.AB.\(cos(\widehat{EBA})\)
11=BE.AB.\(cos(\widehat{EBA})\)
\(cos(\widehat{EBA})=\frac{11}{BE.AB}\)
\(cos(\widehat{EBA})=\frac{11}{\sqrt{5}.\sqrt{37}}\)
\(\widehat{BEA}=Arccos(\frac{11}{\sqrt{5}.\sqrt{37}})\simeq \fbox{36°}\)
Vérifions que la somme des mesures des trois angles vaut 180° : 17+127+36=180°
Question
b. déterminer la longueur AF
Solution
\(\vec{AE}.\vec{AB}=\vec{AF}.\vec{AB}=AF \times AB \times cos 0=AF \times AB=AF \times \sqrt{37}\)
or \(\vec{AE}.\vec{AB}\)=\(AE \times AB \times cos(\widehat{BAE})\)
\(\vec{AE}.\vec{AB}=AE \times AB \times cos(\widehat{BAE})=\sqrt{20} \times \sqrt{37} \times cos(\widehat{BAE})\) or \(\color{red}{cos(\widehat{BAE})=\frac{26}{\sqrt{37}.\sqrt{20}}}\)
donc \(\vec{AE}.\vec{AB}=\sqrt{20} \times \sqrt{37} \times \frac{26}{\sqrt{20} \times \sqrt{37}}=26\) d'après la question précédente.
donc \(AF \times \sqrt{37}=26\)
d'où \(AF=\frac{26}{\sqrt{37}}\simeq 4,27\)