Exercice : Exercice 3 :
On considère un triangle OAB avec OA=5, OB=3 et \((\vec{OA},\vec{OB})=\theta\)
Question
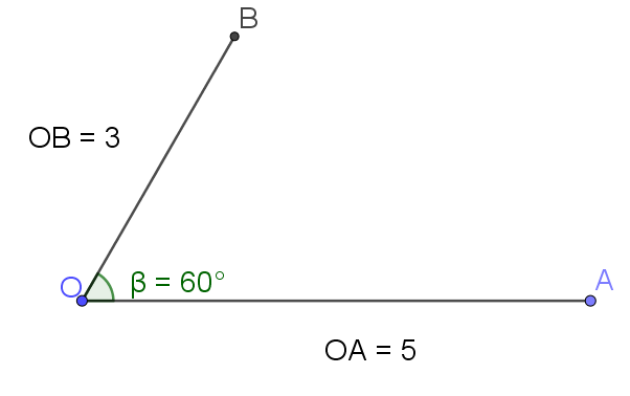
Faire une figure et calculer le produit scalaire \(\vec{OA}.\vec{OB}\) pour \(\theta=\frac{\pi}{3}\)
Solution
\(\vec{OA}.\vec{OB}=\|\vec{OA}\|\times\|\vec{OB}\|\times cos(((\vec{OA},\vec{OB}))\)
\(\vec{OA}.\vec{OB}=5 \times 3 \times cos(\frac{\pi}{3})\)
\(\vec{OA}.\vec{OB}=15 \times \frac{1}{2}=\color{red}{7,5}\)
Question
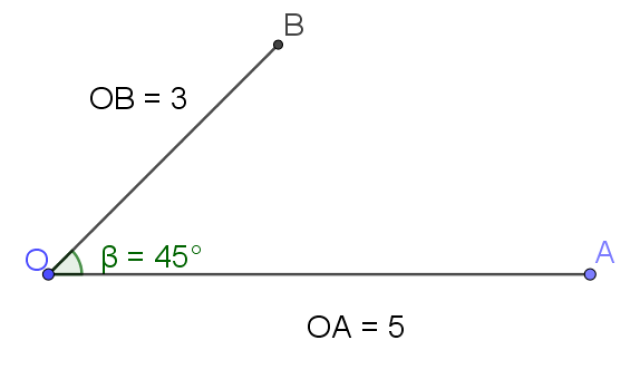
Faire une figure et calculer le produit scalaire \(\vec{OA}.\vec{OB}\) pour \(\theta=\frac{\pi}{4}\)
Solution
\(\vec{OA}.\vec{OB}=\|\vec{OA}\|\times\|\vec{OB}\|\times cos(((\vec{OA},\vec{OB}))\)
\(\vec{OA}.\vec{OB}=5 \times 3 \times cos(\frac{\pi}{4})\)
\(\vec{OA}.\vec{OB}=15 \times \frac{\sqrt{2}}{2}=\color{red}{7,5\sqrt{2}}\)
Question
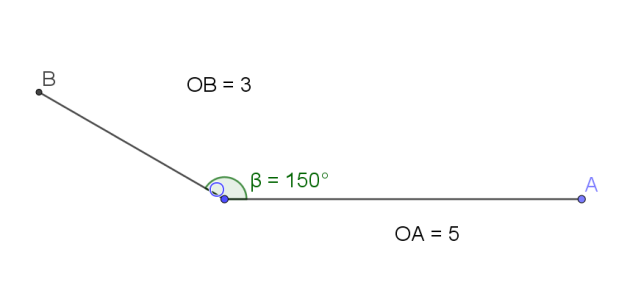
Faire une figure et calculer le produit scalaire \(\vec{OA}.\vec{OB}\) pour \(\theta=\frac{5\pi}{6}\)
Solution
\(\vec{OA}.\vec{OB}=\|\vec{OA}\|\times\|\vec{OB}\|\times cos(((\vec{OA},\vec{OB}))\)
\(\vec{OA}.\vec{OB}=5 \times 3 \times cos(\frac{5\pi}{6})\)
\(\frac{5\pi}{6}=5 \times \frac{\pi}{6}=5 \times 30\mapsto150°\)
\(cos(\frac{5\pi}{6})=cos(\pi-\frac{\pi}{6})=-cos(\frac{\pi}{6})=-\frac{\sqrt{3}}{2}\)
\(\vec{OA}.\vec{OB}=15 \times (-\frac{\sqrt{3}}{2})=\color{red}{-7,5\sqrt{3}}\)