IX.Mesure d'un méridien terrestre par triangulation
Mesure d'un méridien terrestre par triangulation
-230 : ERATOSTHENE ( à Alexandrie) mesure un méridien et donne une bonne valeur approchée du rayon terrestre.
1670 : PICARD mesure par triangulation un arc de méridien entre Amiens et Paris.
1669-1716 :
Les CASSINI mesurent un arc de méridien entre Dunkerque et Collioure d'où il ressort que la terre serait aplatie à l'équateur.
NEWTON déduit du mouvement du pendule à différentes latitudes l'aplatissement aux pôles.
1736-1743 : MAUPERTUIS (en Laponie), BOUGUER et LA CONDAMINE ( au Pérou) vérifient par triangulation l'aplatissement aux pôles.
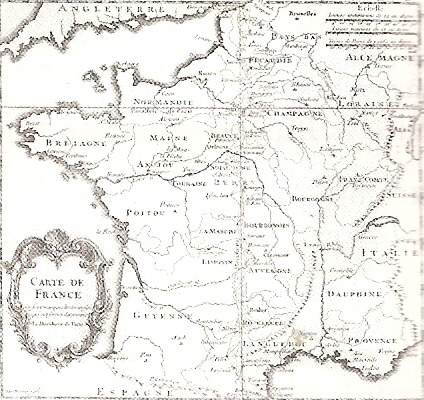
1784 : CASSINI de Thury établit par triangulation une carte précise de la France (180 feuilles)
1791 : DELAMBRE et MECHAIN sont chargés par l'Assemblée Constituante de calculer la longueur de l'arc de méridien Dunkerque-Barcelone afin de définir le mètre comme étant le dix millionième du quart du méridien terrestre.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Complément :

Avant la Révolution, il existait pléthore d'unités de poids et de mesures (250.000) ! Chaque pays, chaque région, et même parfois chaque village, avait les siennes... En 1790 l'Assemblée nationale - désireuse d'effacer toute trace du passé - décide d'établir un système de mesure unique.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Dans La Méridienne, Denis Guedj raconte l'histoire de Delambre et Méchain, chargés entre 1790 et 1798 de mesurer la longueur du méridien joignant Dunkerque à Barcelone afin d'étudier le système métrique.
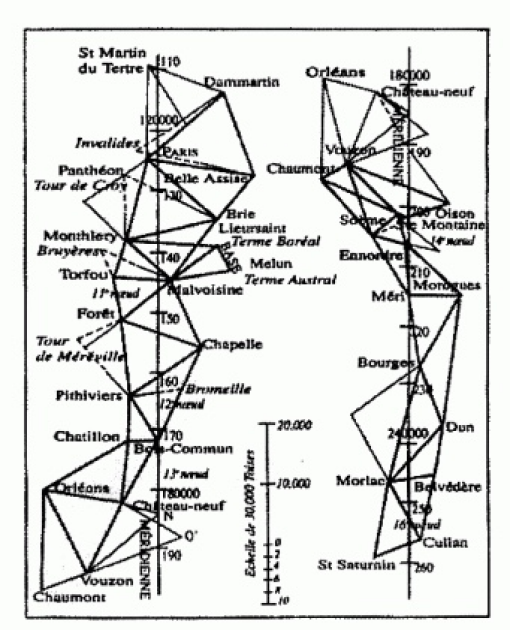
Pour cela, ils créent tout au long du méridien une chaîne de triangles adjacents :
ils mesurent leurs angles et la longueur d'un côté le plus précisément possible.
Puis connaissant les relations métriques dans les triangles, ils en déduisent les longueurs manquantes.
Ils trouvent finalement une longueur égale à 5 130 740 toises.
Jean-Baptiste Joseph Delambre (1749-1822)

Pierre François André Méchain (1744-1804)

Le mètre sera alors défini comme la dix-millionième partie du quart du méridien (1m=0,513 toise).
Par souci de précision cette définition n'a cessé d'être modifiée.
Aujourd'hui le mètre est défini comme la distance parcourue dans le vide par la lumière pendant une durée de \(\frac{1}{299 792 458}\) seconde.
Je vous conseille également la lecture du théorème perroquet de Denis Guedj

Relation des sinus
Fondamental :
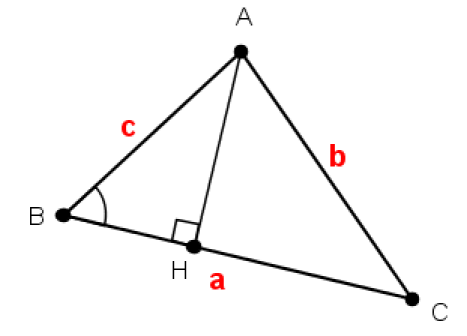
Dans un triangle quelconque ABC, on a les relations suivantes :
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{B}}{b}=\frac{sin \widehat{C}}{c}\)
Complément : Démonstration
La surface du triangle ABC
\(S_{ABC}= \frac{BC \times AH}{2}\)
Or \(sin \widehat{B}=\frac{AH}{AB}=\frac{AH}{c}\)
d'où
\(S_{ABC}= \frac{acsin \widehat{B}}{2}\)
De même on pourrait établir que
\(S_{ABC}= \frac{absin \widehat{C}}{2}\)
\(S_{ABC}= \frac{bcsin \widehat{A}}{2}\)
d'où
\(\frac{acsin \widehat{B}}{2}= \frac{absin \widehat{C}}{2}=\frac{bcsin \widehat{A}}{2}\)
en multipliant par 2 et en divisant par abc, on obtient :
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{B}}{b}=\frac{sin \widehat{C}}{c}\)
Remarque :
Si on connaît les trois angles et a alors la formule des sinus permet de trouver b puis c . Connaître deux angles et un côté permet donc de connaître toutes les mesure d'un triangle.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.

Cercle répétiteur utilisé pour mesurer les angles
Complément :
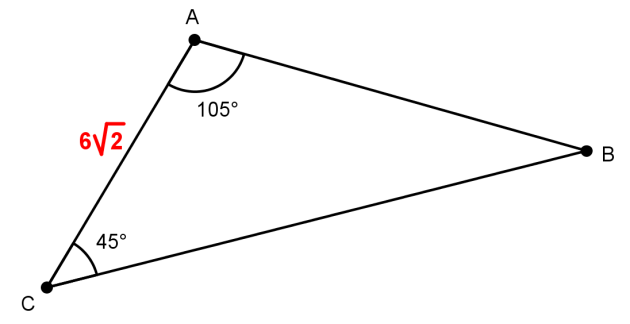
Avec nos notations nous avons alors : \(b = 6\sqrt{2}\)
2, \(\widehat{A}\) = 105° et \(\widehat{C} = 45°\).
On cherche les longueurs AB = c et BC = a
On détermine l'angle \(\widehat{B}\) par complément à 180 :
\(\widehat{B}\)= 180 - 105 - 45 = 30°
En appliquant la relation des sinus, on a :
\(\frac{sin 105}{a}=\frac{sin 30}{6\sqrt{2}}=\frac{sin 45}{c}\)
donc
\(\frac{sin 105}{a}=\frac{sin 30}{6\sqrt{2}}\)
\(\frac{a}{sin 105}=\frac{6\sqrt{2}}{\frac{1}{2}}\)
\(\frac{a}{sin 105}=6\sqrt{2} \times \frac{2}{1}\)
\(a=6\sqrt{2} \times 2 \times sin(105)\)
\(a=12\sqrt{2} sin(105)\)
\(a \simeq 16,39\)
\(\frac{sin 45}{c}=\frac{sin 30}{6\sqrt{2}}\)
\(\frac{c}{sin 45}=\frac{6\sqrt{2}}{\frac{1}{2}}\)
\(\frac{c}{sin 45}=6\sqrt{2} \times \frac{2}{1}\)
\(c=6\sqrt{2} \times 2 \times sin(45)\)
\(c=12\sqrt{2} \times \frac{\sqrt{2}}{2}=6 \times \sqrt{2}^2=6\times 2=12\)
Complément :
C'est sur cette conclusion que s'appuie la méthode utilisée par Méchain et Delambre :
il suffit de n'effectuer qu'une seule mesure linéaire (celle de la base) et une série de mesures angulaires
( beaucoup plus simples à réalisées).
Sa mise en œuvre consiste à recouvrir l'arc de méridien par une chaîne de triangles.