IV. Produit scalaire et norme
Fondamental : Propriété
\(\color{red}{\textbf{Soit } \vec{u} \textbf{ et } \vec{v} \textbf{ deux vecteurs.}}\)
\(\color{red}{ \textbf{On a : }\vec{u}.\vec{v}=\frac{1}{2}(\|\vec{u}\|^2+\|\vec{v}\|^2-\|\vec{u}-\vec{v}\|^2) \textbf{ et }}\)
\(\color{red}{\vec{u}.\vec{v}=\frac{1}{2}(\|\vec{u}+\vec{v}\|^2-\|\vec{u}\|^2-\|\vec{v}\|^2)}\)
Exemple : Démonstration de la première formule :
\(\|\vec{u}-\vec{v}\|^2=\vec{u}^2-2\vec{u} .\vec{v}+\vec{v}^2\)
Donc \(\vec{u}.\vec{v}=\frac{1}{2}(\|\vec{u}\|^2+\|\vec{v}\|^2-\|\vec{u}-\vec{v}\|^2)\)
de même pour la seconde formule avec la seconde identité remarquable.
Fondamental : Propriété
\(\color{red}{\textbf{Soit A, B et C trois points du plan.}}\)
\(\color{red}{\textbf{On a : } \vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AD}\|^2-\|\vec{DB}\|^2)}=\frac{1}{2}(AB^2+AD^2-DB^2)\)
et \(\color{red}{\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}+\vec{AD}\|^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2)}\)
Complément : Démonstration
\(On a : \vec{u}.\vec{v}=\frac{1}{2}(\|\vec{u}\|^2+\|\vec{v}\|^2-\|\vec{u}-\vec{v}\|^2)\) (1)
et \(\vec{u}.\vec{v}=\frac{1}{2}(\|\vec{u}+\vec{v}\|^2-\|\vec{u}\|^2-\|\vec{v}\|^2)\) (2)
Posons :
\(\vec{u}=\vec{AB}\)
\(\vec{v}=\vec{AD}\)
on obtient alors :
\(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AD}\|^2-\|\vec{AB}-\vec{AD}\|^2)\)
\(\vec{AB}-\vec{AD}=\vec{AB}+\vec{DA}=\vec{DB} \)par la relation de Chasles
\(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AD}\|^2-\|\vec{DB}\|^2)\) (1)
et \(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}+\vec{AD}\|^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2)\) (2)
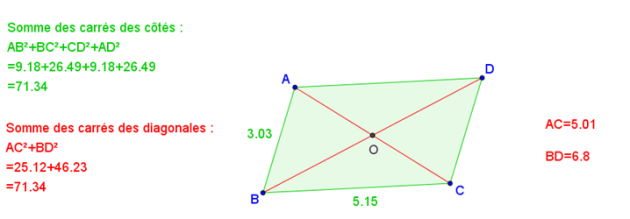
Fondamental : Propriété : Egalité du parallélogramme
\(\color{red}{\textbf{Dans un parallélogramme,la somme des carrés des longueurs }}\)
\(\color{red}{\textbf{des deux diagonales est égale à la somme des carrés des longueurs de ses quatre côtés.}}\)
\(\color{red}{AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2}\)
Complément :
\(On a : \vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}\|^2+\|\vec{AD}\|^2-\|\vec{DB}\|^2)\)
\(\vec{AB}.\vec{AD}=\frac{1}{2}(\|\vec{AB}+\vec{AD}\|^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2)\)
\(\|\vec{AB}\|^2+\|\vec{AD}\|^2-\|\vec{DB}\|^2=\|\vec{AB}+\vec{AD}\|^2-\|\vec{AB}\|^2-\|\vec{AD}\|^2\)
\(2\|\vec{AB}\|^2+2\|\vec{AD}\|^2=\|\vec{AB}+\vec{AD}\|^2+\|\vec{DB}\|^2\)
or \(\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}\)
\(2\|\vec{AB}\|^2+2\|\vec{AC}\|^2=\|\vec{AC}\|^2+\|\vec{DB}\|^2\)
\(2AB^2+2AD^2=AC^2+DB^2\)
AB=DC
AD=BC
donc \(AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2\)
Fondamental : Théorème
\(\color{red}{cos(\vec{u};\vec{v})=\frac{\vec{u}.\vec{v}}{\|\vec{u}\|×\|\vec{v}\|}}\)
Complément :
car \(\vec{u}.\vec{v}= \|\vec{u}\|×\|\vec{v}\|.cos(\vec{u};\vec{v})\)