Exercice : Exercice 5 :
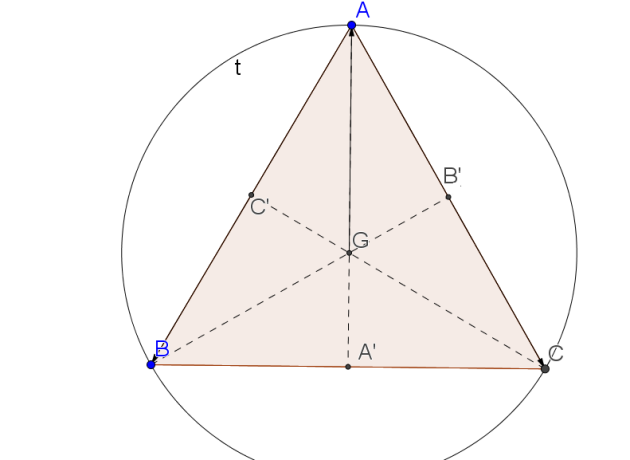
On considère un triangle équilatéral direct ABC tel que AB=4 Soit G son centre de gravité.
Soient A',B',C' les milieux respectifs des segments [BC], [AC], [AB]
Calculer les produits scalaires :
Question
\(1.\vec{AB}.\vec{AC}\)
Solution
\(\vec{AB}.\vec{AC}=\|\vec{AB}\|\times\|\vec{AC}\|\times cos(\vec{AB},\vec{AC})=4 \times 4 \times cos(\frac{\pi}{3})=16 \times \frac{1}{2}=8\)
Question
\(2.\vec{BG}.\vec{BC}\)
Solution
\(\vec{BG}.\vec{BC}=\|\vec{BG}\|\times\|\vec{BC}\|\times cos(\vec{BG},\vec{BC})=\vec{BA'}.\vec{BC}=BA' \times BC=2 \times 4=8\) en effet \(BA'=\|\vec{BG}\| \times cos(\vec{BG},\vec{BC})\)
Question
\(3.\vec{GB}.\vec{GA}\)
Solution
\(\vec{GB}.\vec{GA}\)=\(\vec{GA'}.\vec{GA}=\frac{1}{3}\vec{AA'}\times (\frac{-2}{3}\vec{AA'})=\frac{-2}{9}\|\vec{AA'}\|=\frac{-2}{9}\|\vec{AA'}\|\)
En effet :
\(\color{red}{\textbf{Propriété admise: Les médianes d'un triangle se coupent en un point situé aux} \frac{2}{3} }\)
\(\color{red}{\textbf{de leurs longueurs en partant du sommet dont elles sont issues.}}\)
\(\color{red}{\textbf{Propriété démontrée: La longueur des médianes d'un triangle équilatéral de côtés a est }} \frac{\sqrt{3}a}{2}\)
en effet Dans le cas général pour un triangle équilatéral de longueur de côté : \(a\) , j'utilise le théorème de Pythagore dans le triangle ACA' rectangle en A' :
\(AA'^2+A'C^2=AC^2\)
donc \(AA'^2=AC^2-A'C^2\)
\(AA'^2=a^2-(\frac{a}{2})^2=a^2-\frac{a^2}{4}=\frac{4a^2}{4}-\frac{a^2}{4}=\frac{3a^2}{4}\)
\(AA'^2=a^2-(\frac{a}{2})^2=a^2-\frac{a^2}{4}=\frac{4a^2}{4}-\frac{a^2}{4}=\frac{3a^2}{4}\)
\(AA'=\sqrt{\frac{3a^2}{4}}=\frac{\sqrt{3}a}{2}\)
donc ici \(AA'=\frac{\sqrt{3}\times 4}{2}=2\sqrt{3}\) c'est également la longueur des deux autres médianes.
d'où finalement \(\vec{GB}.\vec{GA}=\frac{-2}{9}\|\vec{AA'}\|=\frac{-2}{9} \times (2\sqrt{3})^2=\frac{-2}{9} \times (2\sqrt{3})^2=\frac{-2}{9} \times (4 \times 3)=\frac{-8}{3}\)
Question
\(4.\vec{AC}.\vec{BA'}\)
Solution
\(\vec{AC}.\vec{BA'} =\vec{A'C}.\vec{BA'}=2\times 2=4\)
Question
\(c.\vec{AC}.\vec{AD}\)
Solution
\(\vec{AC}\vec{AD}=\vec{AB}\vec{AD}=2\sqrt{6}\)
Question
\(5.\vec{GA}.\vec{GB'}\)
Solution
\(\vec{GA}.\vec{GB'}\)
\(=\vec{GB'}.\vec{GB'}\)
\(=\|\vec{GB'}\|^2\)
\(=(\frac{1}{3} \times BB')^2\)
\(=(\frac{1}{3}(2\sqrt{3}))^2\)
\(=\frac{1}{9} \times (4 \times 3)=\frac{4}{3}\)