Exercice : Exercice 19 :
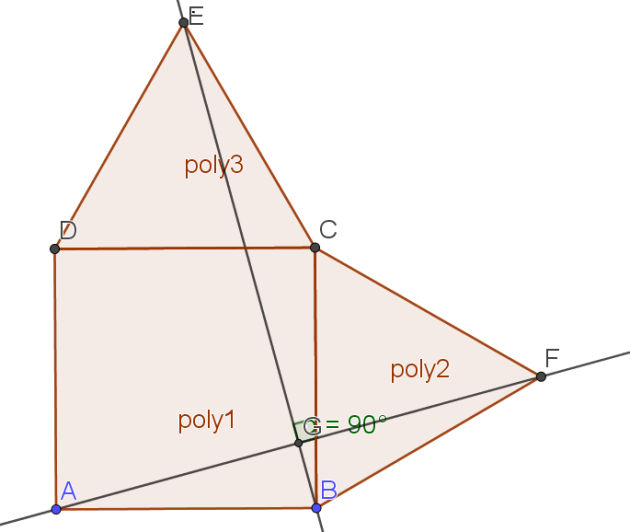
ABCD est un carré.BCF et DCE sont deux triangles équilatéraux extérieurs au carré.
Question
1. Faire une figure
2. On se place dans le repère \((A ;\vec{AB} ;\vec{AD})\)
Question
a. Donner les coordonnées des points de la figure dans ce repère.
Solution
A(0 ;0)
B(1 ;0)
D(0 ;1)
C(1 ;1)
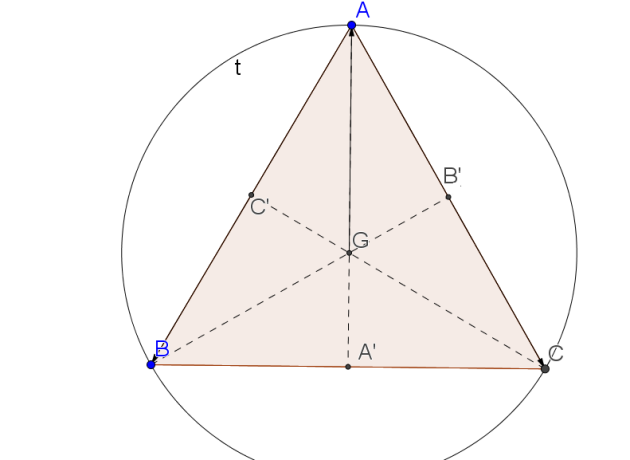
Dans le cas général pour un triangle équilatéral de longueur de côté : \(a\) , j'utilise le théorème de Pythagore dans le triangle ACA' rectangle en A' :
\(AA'^2+A'C^2=AC^2\)
donc \(AA'^2=AC^2-A'C^2\)
\(AA'^2=a^2-(\frac{a}{2})^2=a^2-\frac{a^2}{4}=\frac{4a^2}{4}-\frac{a^2}{4}=\frac{3a^2}{4}\)
\(AA'^2=a^2-(\frac{a}{2})^2=a^2-\frac{a^2}{4}=\frac{4a^2}{4}-\frac{a^2}{4}=\frac{3a^2}{4}\)
\(AA'=\sqrt{\frac{3a^2}{4}}=\frac{\sqrt{3}a}{2}\)
\(E\begin{pmatrix}0,5\\1+\frac{\sqrt{3}}{2}\end{pmatrix} \)en effet la hauteur d'un triangle équilatéral de côté 1 a pour longueur \(\frac{\sqrt{3}}{2}\)
\(F\begin{pmatrix}1+\frac{\sqrt{3}}{2}\\0,5\end{pmatrix} \)en effet la hauteur d'un triangle équilatéral de côté 1 a pour longueur \(\frac{\sqrt{3}}{2}\)
Question
b. Déterminer la mesure de l'angle de vecteurs (\(\vec{AB} ;\vec{AF}\))
Solution
\(\vec{AB}=\left ( \begin{array}{c} x_B-x_A\\ y_B-y_A \end{array} \right )=\left ( \begin{array}{c} 1-0\\ 0-0\end{array} \right )=\left ( \begin{array}{c} 1\\ 0\end{array} \right )\)
\(\vec{AF}=\left ( \begin{array}{c} x_F-x_A\\ y_F-y_A \end{array} \right )=\left ( \begin{array}{c} 1+\frac{\sqrt{3}}{2}-0\\ \frac{1}{2}-0\end{array} \right )=\left ( \begin{array}{c} 1+\frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{array} \right )\)
\(\vec{AB}. \vec{AF}=xx'+yy'\)
\(\Rightarrow \vec{AB}. \vec{AF}=xx'+yy'=1\times (1+\frac{\sqrt{3}}{2})+ 0 \times \frac{1}{2}=1+\frac{\sqrt{3}}{2}\)
\(\vec{AB}. \vec{AF}=||\vec{AB}|| \times ||\vec{AH}||\)
\(\Rightarrow \vec{AB}. \vec{AF}=1 \times (1+\frac{\sqrt{3}}{2})=(1+\frac{\sqrt{3}}{2})\)
\(\vec{AB}. \vec{AF}=||\vec{AB}|| \times ||\vec{AF}|| \times cos((\vec{AB};\vec{AF}))\)
\(||\vec{AB}||=1\)
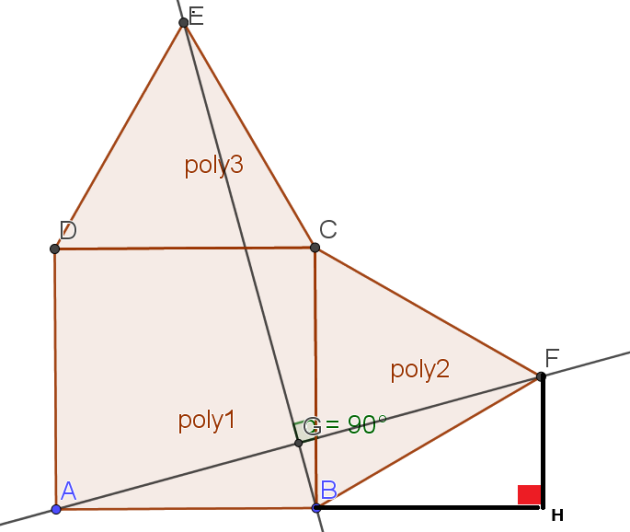
Dans le triangle AHF rectangle en H, d'hypoténuse [AF], d'après le théorème de Pythagore :
\(AF^2=AH^2+HF^2\)
\(\iff AF^2=(1+\frac{\sqrt{3}}{2})^2+(\frac{1}{2})^2\)
\(\iff AF^2=1+2\frac{\sqrt{3}}{2}+(\frac{\sqrt{3}}{2})^2+(\frac{1}{2})^2\)
\(\iff AF^2=1+2\frac{\sqrt{3}}{2}+\frac{3}{4}+\frac{1}{4}\)
\(\iff AF^2=1+2\frac{\sqrt{3}}{2}+\frac{3}{4}+\frac{1}{4}\)
\(\iff AF^2=1+\sqrt{3}+1\)
\(\iff AF^2=2+\sqrt{3}\)
\(\iff AF=\sqrt{2+\sqrt{3}}\)
\(\vec{AB}. \vec{AF}=||\vec{AB}|| \times ||\vec{AF}|| \times cos((\vec{AB};\vec{AF}))\)
\(\Rightarrow \vec{AB}. \vec{AF}=1 \times \sqrt{2+\sqrt{3}} \times cos((\vec{AB};\vec{AF}))\)
\(\iff \vec{AB}. \vec{AF}=1 \sqrt{2+\sqrt{3}} \times cos((\vec{AB};\vec{AF}))\)
\(\vec{AB}. \vec{AF}= \sqrt{2+\sqrt{3}} \times cos((\vec{AB};\vec{AF}))=1+\frac{\sqrt{3}}{2}\)
\(\iff cos((\vec{AB};\vec{AF}))=\frac{1+\frac{\sqrt{3}}{2}}{\sqrt{2+\sqrt{3}}}\)
\(\iff (\vec{AB};\vec{AF}))=Arcos(\frac{1+\frac{\sqrt{3}}{2}}{\sqrt{2+\sqrt{3}}})\)
\(\iff (\vec{AB};\vec{AF}))=Arcos(\frac{1+\frac{\sqrt{3}}{2}}{\sqrt{2}\sqrt{1+\frac{\sqrt{3}}{2}}})\)
\(\iff (\vec{AB};\vec{AF}))=Arcos(\frac{\sqrt{1+\frac{\sqrt{3}}{2}}}{\sqrt{2}})=15°\)
Question
c.Démontrer que les droites (BE) et (AF) sont orthogonales.
Solution
\(\vec{AF}=\begin{pmatrix}1+\frac{\sqrt{3}}{2}-0\\0,5-0\end{pmatrix}\)=\(\begin{pmatrix}1+\frac{\sqrt{3}}{2}\\0,5\end{pmatrix}\)
\(\vec{BE}=\begin{pmatrix}0,5-1\\1+\frac{\sqrt{3}}{2}-0\end{pmatrix}\)=\(\begin{pmatrix}-0,5\\1+\frac{\sqrt{3}}{2}\end{pmatrix}\)
\(\vec{AF}.\vec{BE}=(1+\frac{\sqrt{3}}{2})(-0,5)+0,5 \times (1+\frac{\sqrt{3}}{2})=0\)
donc les vecteurs \(\vec{AF}\) et \(\vec{BE}\) sont orthogonaux et les droites (AF) et (BE) sont perpendiculaires.