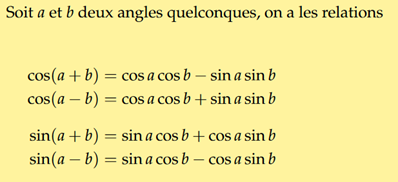VI. Formules d'addition pour les formules de trigonométrie
Exemple :
Le plan est rapporté à un repère orthonormé \((O;\vec{\imath},\vec{\jmath})\)
Soit \(a\) et \(b\) deux nombres réels .
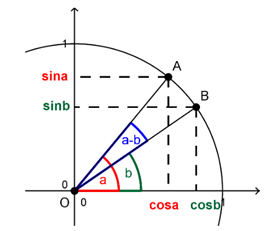
On considère A et B deux points du \(\color{magenta}{\textbf{cercle trigonométrique}}\)
tels que (\(\vec{\imath},\vec{OA}\))=\(a\) (2π) et (\(\vec{\imath},\vec{OB}\))=\(b\) (2π)
1.Déterminer en fonction de a et b une mesure de l'angle \((\vec{OA},\vec{OB})\)
2. En déduire en fonction de a et b, le produit scalaire \(\vec{OA}.\vec{OB}\)
3. Donner dans le repère \((O;\vec{\imath},\vec{\jmath})\), les coordonnées de A et B.
4.En déduire une autre expression de \(\vec{OA}.\vec{OB}\)
5.En comparant les deux expressions du produit scalaire obtenues, démontrer que :
\(\color{red}{cos(a-b)=cos(a)cos(b) + sin(a) sin( b)}\)
En déduire que
Complément :
\(1. (\vec{OA},\vec{OB})=b-a\)
2. \(\vec{OA}.\vec{OB}=\|\vec{OA}\| \times \|\vec{OB}\| \times cos((\vec{OA},\vec{OB}))\)
\(\vec{OA}.\vec{OB}=\|\vec{OA}\| \times \|\vec{OB}\| \times cos(b-a)=1 \times 1 \times cos(b-a)=cos(b-a)\)
3. Coordonnées des points :
\(A(cos(a),sin(a))\)
\(B(cos(b),sin(b))\)
4.\(\vec{OA}=\begin{pmatrix}cos(a)\\sin(a)\end{pmatrix}\)
\(\vec{OB}=\begin{pmatrix}cos(b)\\sin(b)\end{pmatrix}\)
\(\vec{OA}.\vec{OB}=\begin{pmatrix}cos(a)\\sin(a)\end{pmatrix}.\begin{pmatrix}cos(b)\\sin(b)\end{pmatrix}=cos(a).cos(b)+sin(a)sin(b)\)
5.donc \(\color{red}{cos(a-b)=cos a cos b + sin a sin b}\)
Complément : Formules à apprendre par coeur
Ptolémée (Haute-Égypte), né vers 100 - mort vers 168 ap JC
Regiomontanus (Johannes Müller von Königsberg) (Königsberg (Bavière) 6 juin 1436 – Rome 6 juillet 1476)
Complément : Démonstration
1.D'après la démonstration précédente :
\(\color{red}{cos(a-b)=cos(a)cos(b)+sin(a)sin(b)}\)
2.En remplaçant \(b\) par \(-b\), on peut écrire :
\(cos(a-(-b))=cos(a)cos(-b)+sin(a)sin(-b)\)
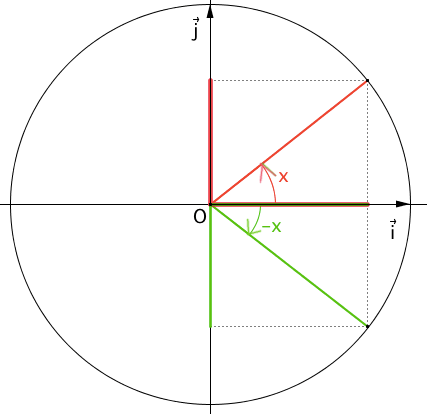
or d'après le dessin ci-dessous, on peut voir que :
\(cos(-b)=cos(b)\) et \(sin(-b)=-sin(b)\)
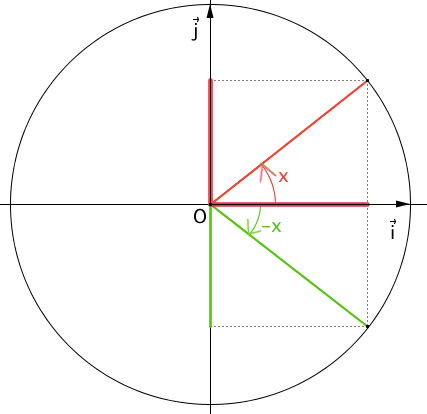
donc \(\color{red}{cos(a+b)=cos(a)cos(b)-sin(a)sin(b)}\)
3. \(cos(\frac{\pi}{2}-x)=sin x\) et \(sin(\frac{\pi}{2}-x)= cos x\)
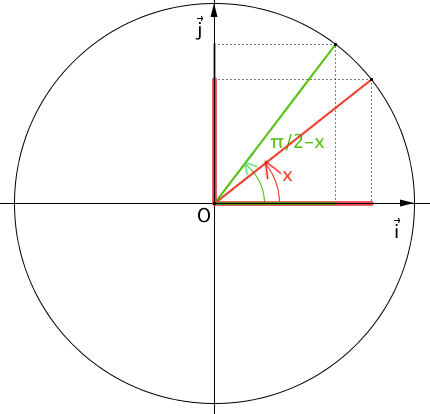
donc \(sin(a+b)=cos(\frac{\pi}{2}-(a+b))\)
d'où \(sin(a+b)=cos(\frac{\pi}{2}-a-b)=cos((\frac{\pi}{2}-a)-b)=cos((\frac{\pi}{2}-a))cos(b)+sin((\frac{\pi}{2}-a))sin(b)=sin(a)cos(b)+cos(a)sin(b)\)
donc \(\color{red}{sin(a+b)=sin(a)cos(b)+cos(a)sin(b)}\)
4.\(sin(a+b)=sin(a)cos(b)+cos(a)sin(b)\)
on remplace \(b\) par \(-b\)
donc \(sin(a+(-b))=sin(a)cos(-b)+cos(a)sin(-b)\)
\(\color{red}{sin(a-b)=sin(a)cos(b)-cos(a)sin(b)}\)
car d'après le dessin ci-dessous, on peut voir que :
\(cos(-b)=cos(b)\) et \(sin(-b)=-sin(b)\)
Fondamental : Formules à apprendre par coeur
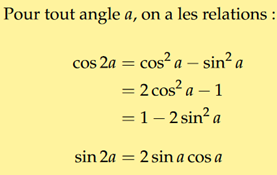
Complément : Démonstration
1.\(\color{red}{cos(a+b)=cos(a)cos(b)-sin(a)sin(b)}\)
on remplace \(b\) par \(a\)
donc \(cos(a+a)=cos(a)cos(a)-sin(a)sin(a)\)
finalement : \(\color{red}{cos(2a)=cos^2(a)-sin^2(a)}\)
2. \(cos^2(a)+sin^2(a)=1\) d'après le chapitre sur la trigonométrie
donc \(sin^2(a)=1-cos^2(a)\)
d'où \(cos(2a)=cos^2(a)-(1-cos^2(a))\)
\(cos(2a)=cos^2(a)-1+cos^2(a)\)
\(\color{red}{cos(2a)=2cos^2(a)-1}\)
3. \(cos^2(a)+sin^2(a)=1\) d'après le chapitre sur la trigonométrie
donc \(cos^2(a)=1-sin^2(a)\)
d'où \(cos(2a)=(1-sin^2(a))-sin^2(a)\)
\(cos(2a)=1-sin^2(a)-sin^2(a)\)
\(\color{red}{cos(2a)=1-2sin^2(a)}\)
4. \(\color{red}{sin(a+b)=sin(a)cos(b)+cos(a)sin(b)}\)
on remplace \(b\) par \(a\)
donc \(sin(a+a)=sin(a)cos(a)+cos(a)sin(a)\)
finalement : \(\color{red}{sin(2a)=2sin(a)cos(a)}\)