Exercice : Exercice 7 :
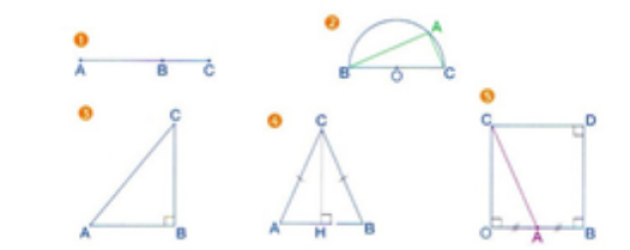
A chacune des figures ci-dessous, associer parmi les égalités suivantes,
celle qui donne le bon résultat pour le calcul de \(\vec{AB}.\vec{AC}\)
1.\( \vec{AB}.\vec{AC}=AB \times AC\)
2.\( \vec{AB}.\vec{AC}=AB^2\)
3.\( \vec{AB}.\vec{AC}=-AB^2\)
4.\( \vec{AB}.\vec{AC}=\frac{1}{2}AB^2\)
5.\( \vec{AB}.\vec{AC}=0\)
Question
a.
Solution
Pour que le produit scalaire \(\vec{AB}\vec{AC}\) soit égal à \(AB \times AC\), il faut que les deux vecteurs \(\vec{AB}\) et \(\vec{AC}\) soient colinéaires donc il s'agit de la figure 1 car \(\vec{AB}\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})\) donc il faut que \(cos(\vec{AB},\vec{AC})=1\) donc que l'angle des deux vecteurs soit nul.
Question
b.
Solution
\(\vec{AB}\vec{AC}=AB^2\) si le \(\vec{AC}\) se projette orthogonalement en \(\vec{AB}\) sur \(\vec{AB}\) donc il s'agit de la figure 3.
Question
c.
Solution
\(\vec{AB}\vec{AC}=-AB^2\) car dans ce cas le \(\vec{AC}\) se projette orthogonalement en \(-\vec{AB}\) sur \(\vec{AB}\) donc il s'agit de la figure 5.
Question
d.
Solution
\(\vec{AB}\vec{AC}=\frac{1}{2}AB^2\) car dans ce cas le \(\vec{AC}\) se projette orthogonalement en \(\frac{1}{2}\vec{AB}\) sur \(\vec{AB}\) donc il s'agit de la figure 4.
Question
e.
Solution
\(\vec{AB}\vec{AC}=0\) si les vecteurs \(\vec{AB}\) et \(\vec{AC}\) sont orthogonaux donc c'est la figure 2.