Exercice : Exercice 31 :
Question
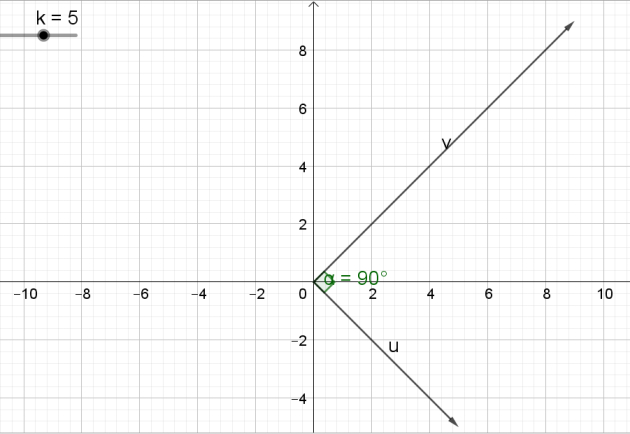
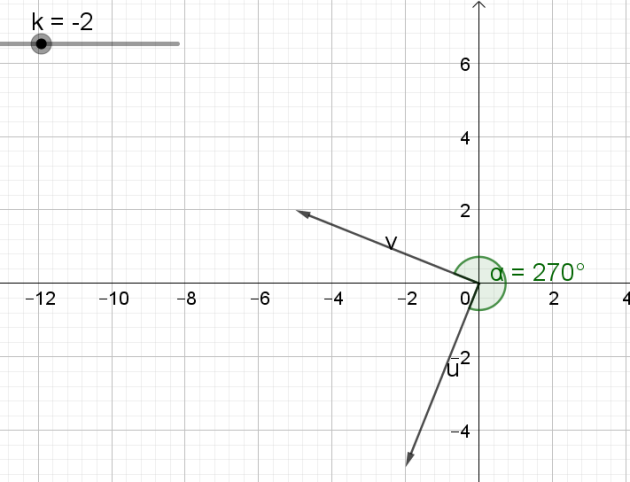
Le plan est rapporté à un repère orthonormé, k est un réel.
Soient \(\vec{u}\)\((k ; -5)\) ,\(\vec{v}\)\((2k-1 ; k+4)\)
Question
Existe-t-il des valeurs du réel k pour lesquelles \(\vec{u}\) et \(\vec{v}\) sont orthogonaux ?\(\)
Solution
\(\vec{u}.\vec{v}=k \times (2k-1)+(-5) \times (k+4)\)
\(\vec{u}.\vec{v}=2k^2-k-5k-20\)
\(\vec{u}.\vec{v}=2k^2-6k-20\)
Les vecteurs \(\vec{u}\) et \(\vec{v}\) sont orthogonaux si leur produit scalaire est nul :
\(\vec{u}.\vec{v}=2k^2-6k-20=0\)
\(2k^2-6k-20=0\)
\(\Delta=b^2-4ac\)
\(\Delta=(-6)^2-4 \times 2 \times (-20)\)
\(\Delta=36+160=196\)
\(k_1=\frac{-b+\sqrt{\Delta}}{2a}\)
\(k_1=\frac{-(-6)+\sqrt{196}}{2\times 2}\)
\(k_1=\frac{-(-6)+14}{4}\)
\(k_1=\frac{6+14}{4}\)
\(k_1=\frac{20}{4}=\fbox{5}\)
\(k_2=\frac{-b-\sqrt{\Delta}}{2a}\)
\(k_2=\frac{-(-6)-\sqrt{196}}{2\times 2}\)
\(k_2=\frac{-(-6)-14}{4}\)
\(k_2=\frac{6-14}{4}\)
\(k_2=\frac{-8}{4}=\fbox{-2}\)