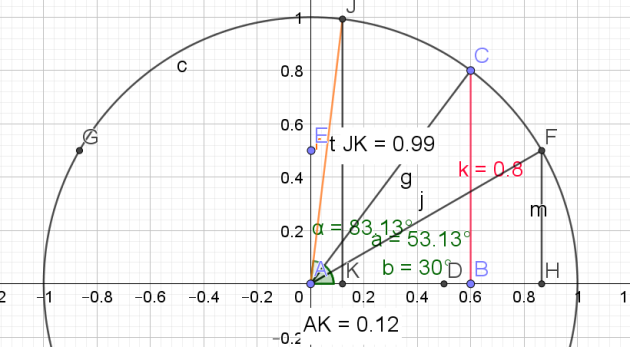
Exercice : Exercice 28 :
a et b sont deux réels de l'intervalle [0;\(\frac{\pi}{2}\)] tel que :
\(cos a = \frac{3}{5}\) et \(sin b =\frac{1}{2}\)
Question
1. Calculer \(sin a\) et \(cos b\).
Solution
Utilisons la relation \(cos^2 x +sin^2x=1\)
\(cos^2 a+sin^2 a =1\)
d'où
\((\frac{3}{5})^2+sin^2 a =1\)
\((\frac{9}{25})+sin^2 a =1\)
\(sin^2 a =1-\frac{9}{25}\)
\(sin^2 a =\frac{25}{25}-\frac{9}{25}\)
\(sin^2 a =\frac{16}{25}\)
\(\color{magenta}{sin a =\frac{4}{5}=0,8}\)
en effet \(sin a\ge0\) car \(a \in[0;\frac{\pi}{2}]\)
de même
\(cos^2b+sin^2 b =1\)
\(cos^2b+(\frac{1}{2})^2 =1\)
\(cos^2 b=1-\frac{1}{4}\)
\(cos^2 b =\frac{4}{4}-\frac{1}{4}\)
\(cos^2 b =\frac{3}{4}\)
\(\color{magenta}{cos b=\frac{\sqrt{3}}{2}}\)
en effet \(cos b\ge0\) car \(b \in[0;\frac{\pi}{2}]\)
Question
2. En déduire \(cos(a + b)\) et \(sin(a + b)\).\(\)
Solution
\(cos(a+b)=cos(a)cos(b)-sin(a)sin(b)=\frac{3}{5}\times \frac{\sqrt{3}}{2}- \frac{4}{5} \times \frac{1}{2}=\frac{3\sqrt{3}}{10}- \frac{4}{10}=\frac{3\sqrt{3}-4}{10}\simeq0,12\)
\(sin(a+b)=sin(a)cos(b)+cos(a)sin(b)=\frac{4}{5}\times \frac{\sqrt{3}}{2}+ \frac{3}{5} \times \frac{1}{2}=\frac{4\sqrt{3}}{10}+ \frac{3}{10}=\frac{4\sqrt{3}+3}{10}\simeq0,99\)