Exercice : Exercice 35 :
Dans le repère orthonormé \((O;\vec{\imath},\vec{\jmath})\)
Question
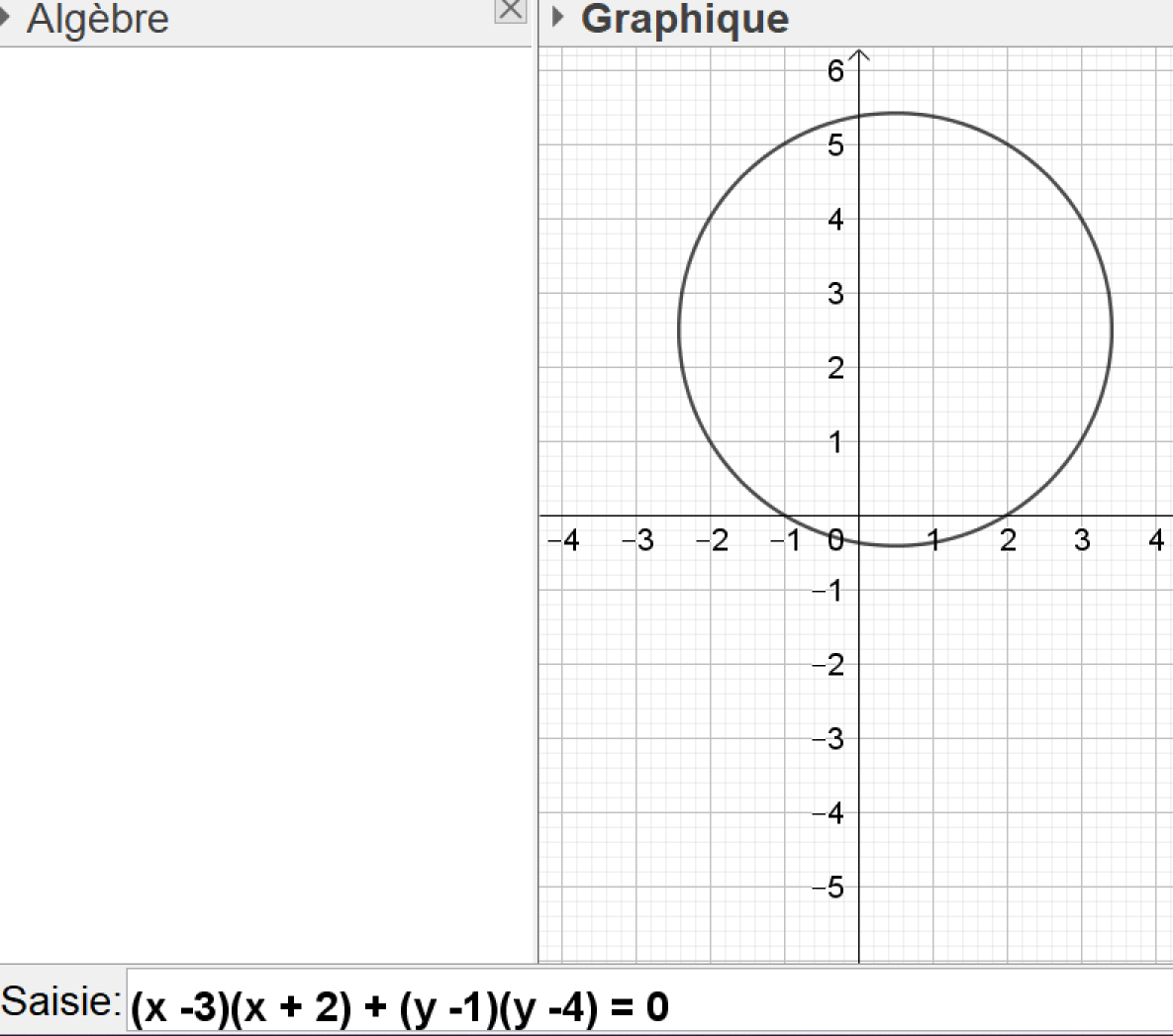
Déterminer l'ensemble des points M du plan dont les coordonnés\( (x ; y)\) vérifient l'équation :
\((x -3)(x + 2) + (y -1)(y -4) = 0\)
Solution
\((x -3)(x + 2) + (y -1)(y -4) = 0\)
\(\Longleftrightarrow \left( \begin{array}{c}x-3 \\y-1\end{array} \right).\left( \begin{array}{c}x+2 \\y-4\end{array} \right)=0\) \(\Longleftrightarrow \vec{AM}.\vec{BM}=0\) ou A(3,1) et B(-2,4)
Les deux vecteurs \(\vec{AM}\) et \(\vec{BM}\) sont donc orthogonaux en M.
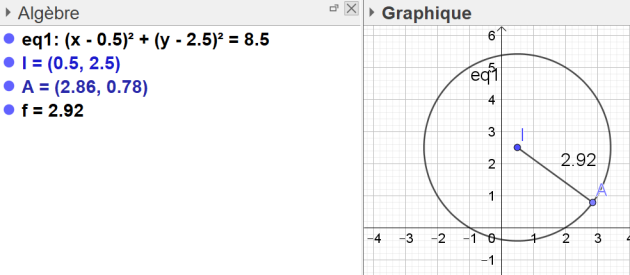
Le triangle ABM est donc rectangle en M.Le point M est donc situé sur le cercle dont un diamètre est [AB].
Le centre du cercle est donc le point I milieu du segment [AB] :
\(x_I=\frac{x_A+x_B}{2}=\frac{3+(-2)}{2}=\frac{1}{2}=0,5\)
\(y_I=\frac{y_A+y_B}{2}=\frac{1+4}{2}=\frac{5}{2}=2,5\)
Le diamètre du cercle est la longueur du segment [AB] :
AB=\(\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-2-3)^2+(4-1)^2}=\sqrt{(-5)^2+(3)^2}=\sqrt{25+9}=\sqrt{34}\)
Le rayon du cercle est la moitié de la longueur du segment [AB] :
\(\frac{AB}{2}\)=\(\frac{\sqrt{34}}{2}=\sqrt{\frac{34}{4}}=\sqrt{8,5}\)
\(\color{magenta}{\textbf{Déterminons l'équation du cercle :}}\)
\(IM^2=R^2\)
\(\sqrt{(x-x_I)^2+(y-y_I)^2}^2=(\sqrt{8,5})^2\)
\((x-0,5)^2+(y-2,5)^2=8,5\)
\(\color{red}{(x-0,5)^2+(y-2,5)^2=8,5}\)