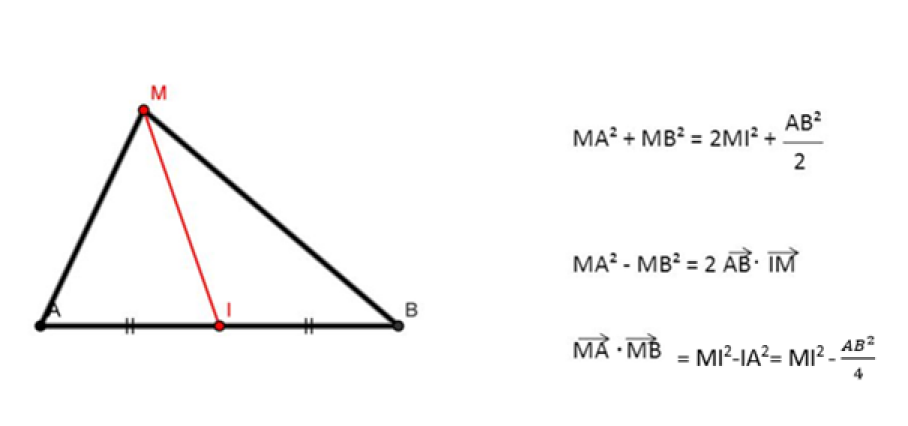
VIII.Théorème de la médiane
Complément :
Complément :
Soit A , B deux points du plan avec \(A \ne B\)
et I le milieu du segment [AB].
Pour tout point M du plan :
Remarque :
On déduit que si M appartient au cercle de centre I
et de diamètre [AB]
\(\vec{MA}.\vec{MB}=0\)
Fondamental : 1ère ligne de niveau
\(\color{red}{MA^2+MB^2=2MI^2+\frac{AB^2}{2}}\)
Complément : Démonstration
\(MA^2+MB^2=(\vec{MA})^2+(\vec{MB})^2=(\vec{MI}+\vec{IA})^2+(\vec{MI}+\vec{IB})^2\)
\(\iff MA^2+MB^2=\vec{MI}^2+2\vec{MI}.\vec{IA}+\vec{IA}^2+\vec{MI}^2+2\vec{MI}.\vec{IB}+\vec{IB}^2\)
\(\iff MA^2+MB^2=MI^2+2\vec{MI}.\vec{IA}+IA^2+MI^2+2\vec{MI}.\vec{IB}+IB^2\) or IA=IB
\(\iff MA^2+MB^2=2MI^2+2\vec{MI}.\vec{IA}+2\vec{MI}.(-\vec{IA})+2IA^2\)
\(\iff MA^2+MB^2=2MI^2+2IA^2\)
\(\iff MA^2+MB^2=2MI^2+2(\frac{AB}{2})^2\)
\(\iff MA^2+MB^2=2MI^2+2\frac{AB^2}{4}\)
\(\iff \color{red}{MA^2+MB^2=2MI^2+\frac{AB^2}{2}}\)
Fondamental : 2ème ligne de niveau
\(\color{red}{MA^2-MB^2=2\vec{AB}.\vec{IM}}\)
Complément : Démonstration
\(MA^2-MB^2=(\vec{MA})^2-(\vec{MB})^2=(\vec{MI}+\vec{IA})^2-(\vec{MI}+\vec{IB})^2\)
\(\iff MA^2-MB^2=\vec{MI}^2+2\vec{MI}.\vec{IA}+\vec{IA}^2-(\vec{MI}^2+2\vec{MI}.\vec{IB}+\vec{IB}^2)\)
\(\iff MA^2-MB^2=\vec{MI}^2+2\vec{MI}.\vec{IA}+\vec{IA}^2-(\vec{MI}^2+2\vec{MI}.\vec{IB}+\vec{IB}^2)\)
\(\iff MA^2-MB^2=MI^2+2\vec{MI}.\vec{IA})+IA^2-MI^2-2\vec{MI}.\vec{IB}-IB^2\) or IA=IB
donc
\(MA^2-MB^2=2\vec{MI}.\vec{IA}-2\vec{MI}.\vec{IB}\)
\(\iff MA^2-MB^2=-2\vec{MI}.\vec{AI}-2\vec{MI}.\vec{IB}\)
\(MA^2-MB^2=-2\vec{MI}.\vec{AI}-2\vec{MI}.\vec{IB}\)
\(\iff MA^2-MB^2=2\vec{IM}.\vec{AI}+2\vec{IM}.\vec{IB}\)
\(\iff MA^2-MB^2=2\vec{IM}.(\vec{AI}+\vec{IB})\)
\(\iff MA^2-MB^2=2\vec{IM}.\vec{AB}\)
\(\iff \color{red}{MA^2-MB^2=2\vec{AB}.\vec{IM}}\)
Fondamental : 3ème ligne de niveau
\(\color{red}{\vec{MA}.\vec{MB}=MI^2-IA^2=MI^2-\frac{AB^2}{4}}\)
Complément : Démonstration
\(\vec{MA}.\vec{MB}=(\vec{MI}+\vec{IA})(\vec{MI}+\vec{IB})\)
\(\iff \vec{MA}.\vec{MB}=\vec{MI}.\vec{MI}+\vec{MI}.\vec{IB}+\vec{IA}.\vec{MI}+\vec{IA}.\vec{IB}\)
\(\iff \vec{MA}.\vec{MB}=MI.MI.cos((\vec{MI},\vec{MI})+\vec{MI}.(-\vec{IA})+\vec{IA}.\vec{MI}+\vec{IA}.(-\vec{IA})\)
\(\iff \vec{MA}.\vec{MB}=MI^2.cos(0)-\vec{IA}.\vec{IA}\)
\(\iff \vec{MA}.\vec{MB}=MI^2-IA.IA.cos(0)\)
\(\iff \vec{MA}.\vec{MB}=MI^2-IA^2\)
\(\iff \vec{MA}.\vec{MB}=MI^2-(\frac{AB}{2})^2\)
\(\iff \color{red}{\vec{MA}.\vec{MB}=MI^2-\frac{AB^2}{4}}\)