Exercice : 2ème ligne de niveau
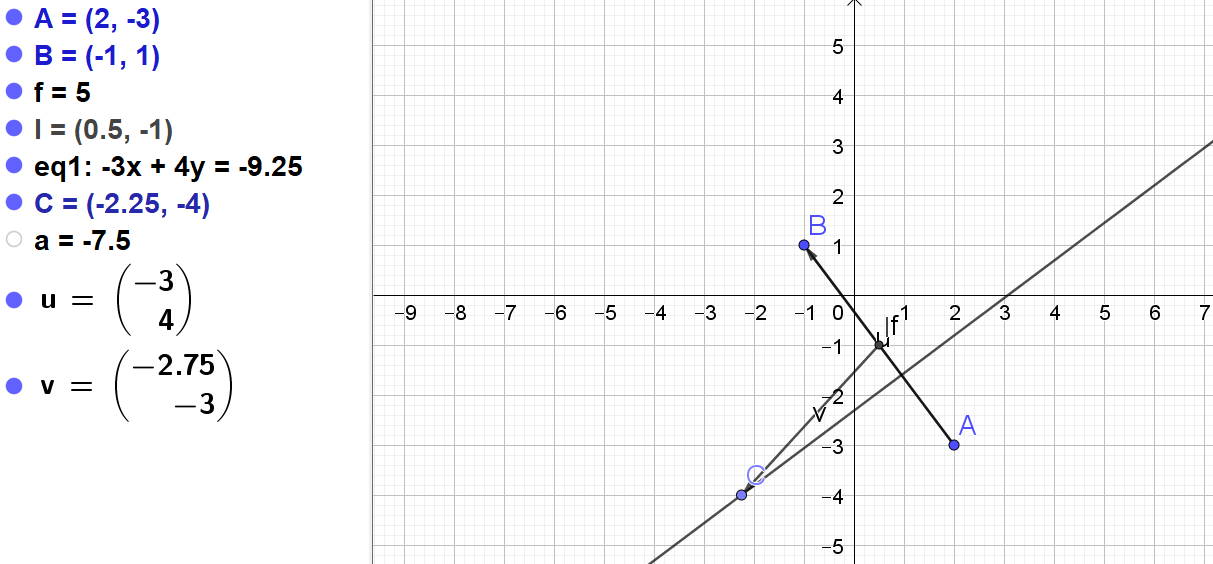
On considère le plan muni d'un repère (O ;I ;J)
les points A et B ont pour coordonnées respectives
(2 ;-3) et (-1 ;1)
On note I le milieu du segment [AB].
M représente un point quelconque du plan et ses coordonnées
sont notées \((x ;y)\)
On s'intéresse au lieu (F) des points définis par :
\(MA^2-MB^2=-7,5\)
Question
1.Déterminer une relation sur les coordonnées des points M appartenant au lieu (F)
Solution
\(MA^2-MB^2=2\vec{AB}.\vec{IM}=-7,5\)
\(\iff 2\vec{AB}.\vec{IM}=-7,5\)
\(x_I=\frac{x_A+x_B}{2}=\frac{2-1}{2}=\frac{1}{2}\)
\(y_I=\frac{y_A+y_B}{2}=\frac{-3+1}{2}=-1\)
\(\iff 2 \left( \begin{array}{c}-1-2\\1-(-3)\end{array} \right). \left( \begin{array}{c}x-\frac{1}{2}\\y-(-1)\end{array}\right)=-7,5\)
\(\iff 2 \left( \begin{array}{c}-3\\4\end{array} \right) . \left( \begin{array}{c}x-\frac{1}{2}\\y+1\end{array}\right)=-7,5\)
\(\iff 2(-3(x-\frac{1}{2})+4(y+1))=-7,5\)
\(\iff -3x+\frac{3}{2}+4y+4=-3,75\)
\(\iff -3x+4y=-3,75-4-\frac{3}{2}\)
\(\iff -3x+4y=-9,25\)
Question
2.Quelle est la nature géométrique de (F) ?Donner les éléments caractéristiques de (F)
Solution
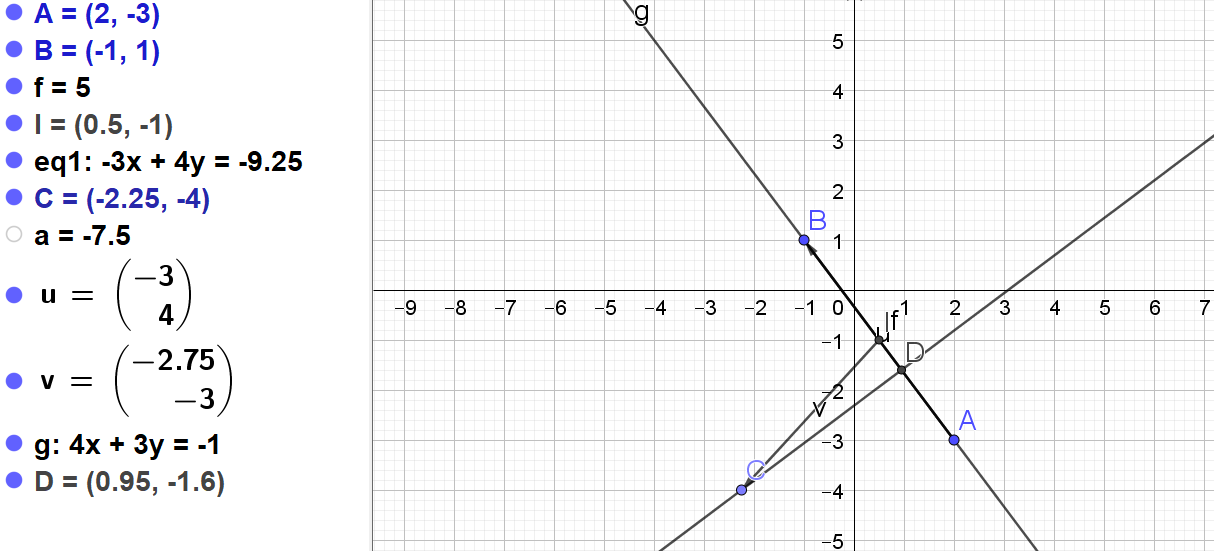
L'ensemble des points (F) est donc une droite perpendiculaire à la droite (AB)
tel que le point H projeté de M sur (AB)
vérifie :
\(2AB.IH=7,5\)
\(\iff 2AB.IH=7,5\)
\(\iff IH=\frac{7,5}{2AB}\)
or
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(\iff AB=\sqrt{(-1-2)^2+(1-(-3))^2}\)
\(\iff AB=\sqrt{(-3)^2+(1+3)^2}\)
\(\iff AB=\sqrt{9+16}\)
\(\iff AB=\sqrt{25}=5\)
\(IH=\frac{7,5}{2 \times 5}=0,75\)
Equation de la droite (AB)
\(a=\frac{y_B-y_A}{x_B-x_A}=\frac{1-(-3)}{-1-2}\)
\(\iff a=\frac{y_B-y_A}{x_B-x_A}=\frac{1+3}{-3}\)
\(\iff a=\frac{1+3}{-3}=\frac{-4}{3}\)
\(y=\frac{-4}{3}x+b\)
or \(A\in (AB)\)
donc
\(1=\frac{-4}{3} \times (-1)+b\)
\(\iff 1=\frac{4}{3}+b\)
\(\iff b=1-\frac{4}{3}\)
\(\iff b=\frac{3}{3}-\frac{4}{3}\)
\(\iff b=-\frac{1}{3}\)
L'équation de la droite (AB) est
donc \(y=\frac{-4}{3}x-\frac{1}{3}\)
ou \(4x+3y=-1\)
\(\begin{cases}-3x+4y=-9,25\\4x+3y=-1\end{cases}\)
\(\iff \begin{cases}-12x+16y=-37\\12x+9y=-3\end{cases}\)
\(25y=-40\)
\(y=\frac{-40}{25}=\frac{-8}{5}=-1,6\)
\(4x+3\times (-1,6)=-1\)
\(4x-4,8=-1\)
\(4x=-1+4,8\)
\(4x=3,8\)
\(x=0,95\)