Exercice : Exercice 40 :
Dans cet exercice, on suppose que les coordonnées de A dans le repère orthonormé sont (3; 2) et que R = 4.
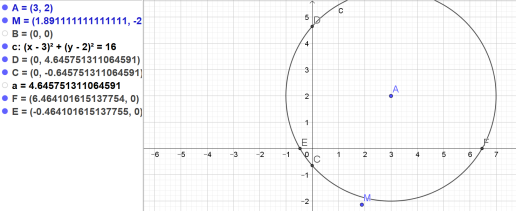
Question
1. Vérifier que la distance entre un point \(M (x; y)\) et le point A est donnée par la formule \(AM =\sqrt{(x- 3)^2 + (y- 2)^2}\)
Solution
\(AM =\sqrt{(x_M- x_A)^2 + (y_M- y_A)^2}\)
\(AM =\sqrt{(x- 3)^2 + (y- 2)^2}\)
Question
2. En déduire que le point M appartient au cercle C si et seulement si\( x^2- 6x + y^2 -4y = 3\):
Solution
\(AM^2=R^2\)
donc \((\sqrt{(x- 3)^2 + (y- 2)^2})^2=(x- 3)^2 + (y- 2)^2=4^2\)
\(\iff (x- 3)^2 + (y- 2)^2=4^2\)
\(\iff x^2- 6x+9 + y^2- 4y+4=16\)
\(\iff x^2- 6x+ y^2- 4y+13=16\)
\(\iff x^2- 6x+ y^2- 4y=16-13\)
\(\iff x^2- 6x+ y^2- 4y=3\)
Question
3. Calculer les coordonnées des points d'intersection du cercle \(C\) et de l'axe des ordonnées.
Solution
Points d'intersection entre l'axe des ordonnées et le cercle C:
\(\begin{cases}{x=0\\x^2- 6x+ y^2- 4y=3}\end{cases}\)
\(0^2-6\times 0+y^2-4y=3\)
\(y^2-4y=3\)
\(y^2-4y-3=0\)
\(\Delta=b^2-4ac=(-4)^2-4\times 1 \times (-3)=16+12=28\)
\(\sqrt{\Delta}=\sqrt{28}=\sqrt{4\times 7}=2\sqrt{7}\)
\(y_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-4)-2\sqrt{7}}{2\times 1}=\frac{4-2\sqrt{7}}{2}=2-\sqrt{7}\simeq-0,65\) \(\mapsto C(0 ;-0,65)\)
\(y_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-4)+2\sqrt{1}}{2\times 1}=\frac{4+2\sqrt{7}}{2}=2+\sqrt{7}\simeq4,65\) \(\mapsto D(0 ;4,65 )\)
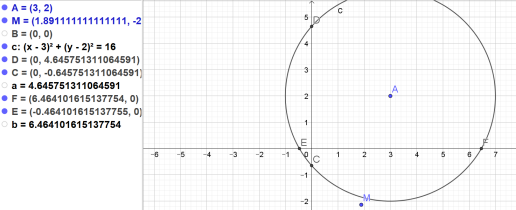
Question
4. Calculer les coordonnées des points d'intersection du cercle \(C\) et de l'axe des abscisses.
Soient les points B(0; 6) et C(6; 0).
Solution
Points d'intersection entre l'axe des abscisses et le cercle C:
\(\begin{cases}{y=0\\x^2- 6x+ y^2- 4y=3}\end{cases}\)\(\)
\(x^2-6x+0^2-4 \times 0=3\)
\(x^2-6x=3\)
\(x^2-6x-3=0\)
\(\Delta=b^2-4ac=(-6)^2-4\times 1 \times (-3)=36+12=48\)
\(\sqrt{\Delta}=\sqrt{48}=\sqrt{3\times 16}=4\sqrt{3}\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-6)-4\sqrt{3}}{2\times 1}=\frac{6-4\sqrt{3}}{2}=3-2\sqrt{3}\simeq-0,46\mapsto E(-0,46 ;0)\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-6)+2\sqrt{1}}{2\times 1}=\frac{6+4\sqrt{3}}{2}=3+2\sqrt{3}\simeq6,46\mapsto F(6,46 ;0)\)
